Zufallsbits
Pseudozufallsbits mit linear rückgekoppeltem Schieberegister
Echte Zufallsbits lassen sich nur durch physikalische Prozesse (Münzwurf, radioaktiver Zerfall, thermisches Rauschen) erzeugen. Mithilfe mathematischer Methoden lassen sich jedoch Pseudozufallsbits gewinnen, die ähnliche Eigenschaften wie echte Zufallsbits haben.
Pseudozufallsbits
Zur Erzeugung einer pseudozufälligen Bitfolge eignen sich linear rückgekoppelte Schieberegister (Linear Feedback Shift Register – LFSR). Das folgende Bild zeigt ein linear rückgekoppeltes Schieberegister mit n = 4 Stellen; diese seien mit r1, r2, r3, r4 ∈ {0, 1} vorbesetzt. Diese Werte werden mit konstanten Werten a1, a2, a3, a4 ∈ {0, 1} multipliziert (logisches Und) und anschließend modulo 2 addiert (logisches Exklusiv-Oder). Das Ergebnis wird im nächsten Takt an die Stelle von r1 übernommen; die vorherigen Werte werden alle um eine Stelle nach links weitergeschoben, r4 wird ausgegeben (Bild 1).
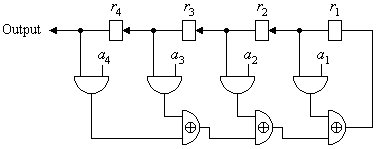
Bild 1: Prinzip eines linear rückgekoppelten Schieberegisters
Beispiel: Es sei n = 4 sowie a1 = 1, a2 = 0, a3 = 0, a4 = 1. Dies führt zu folgendem vereinfachten Schaltbild (Bild 2):
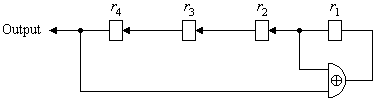
Bild 2: Vereinfachte Schaltung
Wird das Schieberegister mit r1 = 1 initialisiert, so durchläuft es nacheinander die 15 Belegungen
Die Ausgabefolge 0 0 0 1 1 1 1 0 1 0 1 1 0 0 1 ist die gewünschte Pseudozufallsfolge.
Satz: Ein linear rückgekoppeltes Schieberegister der Länge n kann maximal 2n-1 verschiedene Zustände annehmen.
Beweis: Jeder Zustand des linear rückgekoppelten Schieberegisters entspricht einer Belegung seiner n Stellen mit Nullen und Einsen. Es gibt 2n verschiedene solche Belegungen. Ist das Schieberegister nur mit Nullen belegt, so bleibt es stets in diesem Zustand. Enthält es mindestens eine Eins, so verbleiben maximal 2n-1 mögliche Folgezustände.
Satz: Die Ausgabefolge eines linear rückgekoppelten Schieberegisters der Länge n ist periodisch mit maximaler Periode 2n-1.
Beweis: Der Zustandsübergangsgraph eines linear rückgekoppelten Schieberegisters ist ein Kreis, da jeder Zustand eindeutig vom vorherigen Zustand bestimmt wird. Das jeweilige Ausgabebit hängt nur vom Zustand des Schieberegisters ab. Die Folge der Ausgabebits ist also bei jedem Durchlauf durch den Kreis dieselbe, d.h. sie ist periodisch. Die maximale Länge der Periode ist 2n-1, da der Kreis maximal 2n-1 Zustände enthält.
Definition: Das charakteristische Polynom eines linear rückgekoppelten Schieberegisters ist definiert als
p = anxn ⊕ . . . ⊕ a1x ⊕ 1
Definition: Ein Polynom vom Grad n heißt primitiv, wenn es
- unzerlegbar ist und
- es kein Teiler von xd ⊕ 1 ist für alle d < 2n-1
Satz: Ein linear rückgekoppeltes Schieberegister der Länge n nimmt genau dann alle 2n-1 möglichen Zustände an, wenn sein charakteristisches Polynom primitiv ist.
Das charakteristische Polynom des linear rückgekoppelten Schieberegisters aus obigem Beispiel ist p = x4 ⊕ x ⊕ 1; es ist primitiv, da das Schieberegisters alle 24-1 = 15 möglichen Zustände annimmt.
Pseudozufallsbits und Kryptografie
Es liegt nahe, Pseudozufallsbits anstelle echter Zufallsbits zur Verschlüsselung von binär codierten Nachrichten zu verwenden (One-Time-Pad). Hierbei ergibt sich der Geheimtext c = c1 ... ck als bitweise Summe modulo 2 (Exklusiv-Oder) aus dem Klartext m = m1 ... mk und der Zufallsfolge r = r1 ... rk :
ci = mi ⊕ ri für i = 1, ..., k
Besteht die Folge r aus echten Zufallsbits, so ist die Verschlüsselung absolut sicher. Besteht die Folge r dagegen aus Pseudozufallsbits, die von einem linear rückgekoppelten Schieberegister der Länge n erzeugt wurden, so ist die Verschlüsselung absolut unsicher. Bereits die Kenntnis von 2n beliebigen aufeinanderfolgenden Bits reicht aus, um die Konstanten a1, ..., an des linear rückgekoppelten Schieberegisters und damit die gesamte Pseudozufallsfolge zu bestimmen. Die 2n Pseudozufallsbits lassen sich bestimmen, wenn 2n aufeinanderfolgende Klartextbits zusammen mit den zugehörigen Geheimtextbits bekannt sind (known plaintext attack) oder aufgrund eines im Klartext wahrscheinlich vorkommenden Wortes erraten werden können.
Zur Bestimmung der Konstanten des linear rückgekoppelten Schieberegisters müssen lediglich n Gleichungen mit den n Unbekannten a1, ..., an aufgelöst werden.
Beispiel: Es sei n = 4, und eine zusammenhängende Folge r1, ..., r8 von Pseudozufallsbits sei bekannt. Wenn die 4 Stellen des Schieberegisters mit r5, ..., r8 belegt sind (von rechts nach links), dann wird r8 ausgegeben (Bild 3).
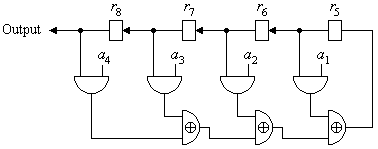
Bild 3: Belegung des linear rückgekoppelten Schieberegisters
Anschließend ist das Schieberegister mit r4, ..., r7 belegt, wobei für das rechts hereingeschobene r4 gilt:
a4·r8 ⊕ a3·r7 ⊕ a2·r6 ⊕ a1·r5 = r4
Aus den Belegungen des Schieberegisters in den nächsten drei Takten ergeben sich als weitere Gleichungen:
a4·r7 ⊕ a3·r6 ⊕ a2·r5 ⊕ a1·r4 = r3
a4·r6 ⊕ a3·r5 ⊕ a2·r4 ⊕ a1·r3 = r2
a4·r5 ⊕ a3·r4 ⊕ a2·r3 ⊕ a1·r2 = r1
Aus diesen 4 Gleichungen lassen sich die 4 Unbekannten a1, ..., a4 berechnen.
Sind die Konstanten des linear rückgekoppelten Schieberegisters ermittelt, lässt sich die Folge aller folgenden und, durch entsprechendes Zurückrechnen, aller vorherigen Pseudozufallsbits bestimmen und damit der gesamte Geheimtext entschlüsseln. Für kryptografische Anwendungen sind also durch linear rückgekoppelte Schieberegister erzeugte Pseudozufallsbits absolut ungeeignet. In der Kryptografie werden kryptografisch sichere Zufallsbits benötigt, die auf andere Art und Weise erzeugt werden.
Literatur
[Wel 88] D. Welsh: Codes and Cryptography. Oxford University Press (1988)
[PP 16] C. Paar, J. Pelzl: Kryptografie verständlich. Springer Vieweg (2016)
[Lan 18] H.W. Lang: Kryptografie für Dummies. Wiley (2018)
Weiter mit: [Blum-Micali-Zufallsbits] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 12.02.2001 Updated: 17.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
