Datenanalyse
Neuronales Netz
Neuronale Netze versuchen die Vernetzung der Neuronen im Gehirn nachzubilden. Sie sind damit ein Verfahren der künstlichen Intelligenz (KI).
Bild 1 zeigt ein neuronales Netz mit drei Schichten von Neuronen. In dieser Darstellung fließen die Daten von oben nach unten durch das Netz. Jedes Neuron bildet die Summe der an seinen Eingängen anliegenden Werte und berechnet daraus ein Aktivierungspotenzial. Diesen Wert gibt es an alle Neuronen der nächsten Schicht weiter, jeweils mit einem gewissen Faktor gewichtet. Das "Wissen" des neuronalen Netzes, welches es in der Trainingsphase ansammelt, besteht aus nichts anderem als den Werten dieser Gewichte.
Bevor also ein neuronales Netz etwas Sinnvolles tun kann, muss es trainiert werden. In der Trainingsphase oder auch Lernphase werden in der Eingabeschicht bestimmte Werte eingegeben. Dann wird kontrolliert, was das neuronale Netz in der Ausgabeschicht ausgibt, und dies wird mit dem gewünschten Ergebnis verglichen. Die Abweichung wird in das neuronale Netz zurückgespeist (backpropagation), um die Werte der Gewichte zu verbessern. Das Ganze wird zig-tausend Mal mit unterschiedlichen Werten wiederholt, um die Gewichte immer feiner auszutarieren. Die Trainingsphase eines neuronalen Netzes ist entsprechend rechenaufwendig.
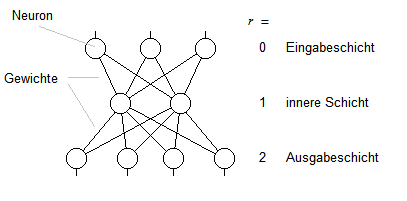
Bild 1: Neuronales Netz mit drei Schichten
Vorwärtspropagation
An den Eingängen der Neuronen der Eingabeschicht wird ein Muster eingegeben, dies ist ein Vektor von reellen Zahlen, der Eingabevektor. Die Neuronen der Eingabeschicht berechnen daraus jeweils für sich ein Aktivierungspotenzial, dies ist eine reelle Zahl zwischen 0 und 1. Diesen Wert geben sie über die Verbindungen an die Neuronen der nächsten Schicht weiter.
Die Verbindungen zwischen Neuronen sind mit reellen Zahlen gewichtet. Die Neuronen der jeweils nächsten Schicht bilden somit die Summe der gewichteten Aktivierungspotenziale der Neuronen der vorherigen Schicht. Aus diesem Wert berechnen sie jeweils ebenfalls ihr Aktivierungspotenzial. Genauso geht es dann zur nächsten Schicht weiter.
Die Neuronen der Ausgabeschicht zeigen an ihren Ausgängen jeweils ihr Aktivierungspotenzial. Zusammengenommen ergibt sich ein Ausgabevektor. Anhand dieses Ausgabevektors soll das neuronale Netz das Muster, das eingegeben wurde, erkennen. Genauer gesagt soll es unterschiedliche ähnliche Muster klassifizieren, also beispielsweise handgeschriebene Ziffern den Werten 0, ..., 9 zuordnen.
Schwellenwertfunktion σ
Die Neuronen berechnen ihr Aktivierungspotenzial aus der Summe ihrer Eingabewerte mit einer Art von Schwellenwertfunktion σ. Das Aktivierungspotenzial der einzelnen Neuronen wird dadurch auf einen Wert zwischen 0 und 1 normalisiert. Häufig wird für σ die folgende Funktion gewählt:
| 1 |
| 1 + e-x |
Bild 2 zeigt die Funktion σ(x).

Bild 2: Funktion σ(x) = 1 / (1 + e-x)
Bezeichnungsweisen
Für die mathematische Formulierung der Berechnungen und später für die Implementierung als Computerprogramm sind sehr genaue Bezeichnungsweisen erforderlich; diese werden im Folgenden angegeben.
Schön ist es nicht, aber im Folgenden notwendig, nämlich Indizes hochgestellt zu schreiben. Während untere Indizes auf die Komponenten einer Struktur verweisen, dient der obere Index dazu, diese Strukturen zu unterscheiden. Hier sind diese Strukturen die Schichten des neuronalen Netzes, und die Komponenten sind die einzelnen Neuronen dieser Schicht. Somit wird beispielsweise der Ausgabewert des Neurons j in Schicht r mit sj(r) bezeichnet. Obere Indizes stehen dabei immer in Klammern, um Verwechslungen mit Exponenten zu vermeiden.
Bezeichnungen
| n | Anzahl der Schichten des neuronalen Netzes | |
| m(r) | Anzahl der Neuronen in Schicht r, r ∈ {0, ..., n-1} | |
| ej(r) | Eingabewert für Neuron j in Schicht r | |
| sj(r) | Ausgabewert für Neuron j in Schicht r | |
| wi,j(r-1) | Gewichtung der Verbindung zwischen Neuron i in Schicht r-1 und Neuron j in Schicht r | |
| xj | Eingabewert für Neuron j in Schicht 0 | |
| yj | Zielwert für den Ausgabewert von Neuron j in der Ausgabeschicht n-1 | |
| fj | Fehlerwert für Neuron j in der Ausgabeschicht n-1 | |
| g | Gesamtfehler der Ausgabeschicht |
Formeln
Der Eingabewert ej(0) eines Neurons in Schicht 0 ist gleich dem Eingabewert xj:
ej(0) = xj
Der Eingabewert ej(r) eines Neurons j in Schicht r > 0 ergibt sich als gewichtete Summe aller Ausgabewerte der Neuronen der vorherigen Schicht r-1:
ej(r) =  k=0, ..., m(r-1)-1 sk(r-1) · wk,j(r-1)
k=0, ..., m(r-1)-1 sk(r-1) · wk,j(r-1)
Der Ausgabewert sj(r) eines Neurons j in Schicht r ergibt sich durch Anwendung der Schwellenwertfunktion σ auf den Eingabewert ej(r):
sj(r) = σ(ej(r))
Der Fehlerwert fj für Neuron j in der Ausgabeschicht n-1 ist die quadratische Abweichung zwischen Ausgabewert sj(n-1) und Zielwert yj:
fj = 1/2·(sj(n-1) – yj)2
Der Gesamtfehler g der Ausgabeschicht ist gleich der Summe aller Einzelfehler fj
g =  j = 0, ..., m(n-1) fj
j = 0, ..., m(n-1) fj
Vektorschreibweise
Die Werte in den einzelnen Schichten lassen sich als Vektoren schreiben. In Vektorschreibweise lassen sich die jeweiligen Berechnungen sehr viel übersichtlicher darstellen. So ist beispielsweise der Ausgabevektor S(r) einer Schicht r gleich
S(r) = s0(r), ..., sm(r)-1(r)
Er wird als Zeilenvektor bzw. als 1×m(r)-Matrix aufgefasst.
Berechnungen in Vektorschreibweise lassen sich mithilfe der Python-Bibliothek numpy direkt in Programme überführen.
| E(r) | Eingabevektor in Schicht r | |
| S(r) | Ausgabevektor in Schicht r | |
| W(r-1) | die m(r-1)×m(r)-Matrix der Gewichtungen zwischen Schicht r-1 und Schicht r | |
| X | Eingabevektor in Schicht 0 | |
| Y | Zielvektor für die Ausgabeschicht n-1 | |
| F | Fehlervektor in der Ausgabeschicht n-1 |
Trainieren des neuronalen Netzes
Zum Trainieren des neuronalen Netzes werden nacheinander unterschiedliche Eingabevektoren X in das neuronale Netz eingegeben und per Vorwärtspropagation jeweils die Aktivierungspotenziale der folgenden Schichten berechnet. Es wird beobachtet, wie gut sich das entsprechende Aktivierungspotenzial der Ausgabeschicht dem jeweils zugehörigen Zielvektor Y annähert.
Die Vorwärtspropagation ist nichts anderes als die Berechnung des Ausgabevektors S(n-1) aus einem Eingabevektor X.
Vorwärtspropagation
Eingabe:
Neuronales Netz mit n Schichten, Eingabevektor X
Methode:
- setze E(r) = S(r-1) · W(r-1)
setze E(0) = X
setze S(0) = σ(E(0))
für r = 1 bis n-1
setze S(r) = σ(E(r))
Hierbei ergibt sich der jeweils nächste Eingabevektor E(r) einer Schicht r des neuronalen Netzes durch Matrixmultiplikation zwischen der 1×m(r-1)-Matrix S(r-1) und der m(r-1)×m(r)-Matrix W(r-1). Das Ergebnis ist die 1×m(r)-Matrix E(r).
Die Funktion σ wird komponentenweise auf den jeweiligen Eingabevektor E(r) angewandt.
Programm für die Vorwärtspropagation
Die entsprechende Funktion für die Vorwärtspropagation lautet in der Programmiersprache Python wie folgt. Zuvor wird die Python-Bibliothek numpy eingebunden.
# Vorwärtspropagation eines Eingabevektors X
# durch ein neuronales Netz mit n Schichten
def propagate(x):
e[0]=np.array(x).reshape(1,m[0]) # 1 x m[0]-Matrix
s[0]=sigma(e[0])
for r in range(1, n):
e[r]=np.matmul(s[r-1], w[r-1])
s[r]=sigma(e[r])
Die Funktion σ lässt sich in Python folgendermaßen implementieren:
return 1.0/(1+np.exp(-x))
Damit das neuronale Netz lernt, wird in der Trainingsphase nach jeder Vorwärtspropagation eines Eingabevektors der Ausgabevektor mit den bekannten Zielwerten verglichen und daraus eine Anpassung der Gewichtungen berechnet.
Im Anschluss an die Trainingsphase, wenn das neuronale Netz gut gelernt hat, kann es Eingabevektoren mit unbekannten Zielwerten verarbeiten.
Anpassung der Gewichtungen zwischen Schicht 1 und Schicht 2
Es geht darum, die Abweichung zwischen den Aktivierungspotenzialen der Ausgabeschicht und den Zielwerten auszuwerten und anschließend die Gewichtungen des neuronalen Netzes so anzupassen, dass ein Lerneffekt eintritt. Dieser Vorgang wird als Backpropagation (etwa Zurückverbreiten, Rückspeisung) bezeichnet.
Im Folgenden wird ein neuronales Netz mit n = 3 Schichten betrachtet, mit einer Eingabeschicht 0, einer inneren Schicht 1 und einer Ausgabeschicht 2. Damit wird die Indizierung mit den oberen Indizes anschaulicher. Die Verallgemeinerung auf ein neuronales Netz mit mehreren inneren Schichten ist zum Schluss angegeben.
Wenn das neuronale Netz während der Lernphase noch nicht die richtigen Ausgabewerte liefert, müssen die Gewichtungen angepasst werden. Dies geschieht in Abhängigkeit von den Fehlern fj(2), die an den Neuronen der Ausgabeschicht 2 auftreten.
Zunächst werden die Gewichtungen wi,j(1) zwischen Schicht 1 und Schicht 2 angepasst. Die Gewichtungen wk,i(0) zwischen Schicht 0 und Schicht 1 werden später angepasst.
Ziel ist es, die Fehlerfunktion g abhängig von den einzelnen Gewichtungen zu minimieren. Hierzu wird die Methode des Gradientenabstiegs verwendet. Gesucht ist der Gradient, also die Steigung der Fehlerfunktion g in Abhängigkeit von der Gewichtung wi,j(1), mit dem Ziel, die Gewichtung in Richtung des Gradienten anzupassen. Die Steigung wird durch die partielle Ableitung von g nach wi,j(1) berechnet.
Da g abhängig ist von fj(2), dieses wiederum von sj(r) und dieses wiederum von ej(r), wird die Ableitung mithilfe der Kettenregel durchgeführt. Die Ableitung der Funktion σ(x) ist
σ'(x) = σ(x) · (1 – σ(x))
Dies wird bei der Anwendung der Kettenregel benutzt; die Herleitung ist weiter unten angegeben.
Es folgt die Berechnung der partiellen Ableitung des Gesamtfehlers g nach einer Gewichtung wi,j(2).
Die Formeln mit den partiellen Ableitungen erschließen sich nicht beim schnellen Überfliegen – tatsächlich ist es aber nicht schwierig, sich Schritt für Schritt hindurchzuarbeiten.
| ∂g |
| ∂wi,j(1) |
| ∂g |
| ∂fj(2) |
| ∂fj(2) |
| ∂sj(2) |
| ∂sj(2) |
| ∂ej(2) |
| ∂ej(2) |
| ∂wi,j(1) |
Für die einzelnen Ableitungen in der Kette gilt:
| ∂g |
| ∂fj(2) |
| ∂ |
| ∂sj(r) |
 t = 0, ..., m(2)-1 ft(2)ungleich 0 nur für t = j = 1
t = 0, ..., m(2)-1 ft(2)ungleich 0 nur für t = j = 1
| ∂fj(2) |
| ∂sj(2) |
| ∂ |
| ∂sj(2) |
| ∂sj(2) |
| ∂ej(2) |
| ∂ |
| ∂ej(2) |
| ∂ej(2) |
| ∂wi,j(1) |
| ∂ |
| ∂wi,j(1) |
 t = 0, ..., m(1)-1 st(1) · wt,j(1)wi,j(1) ist eines der wt,j(1) mit t = i = si(1)
t = 0, ..., m(1)-1 st(1) · wt,j(1)wi,j(1) ist eines der wt,j(1) mit t = i = si(1)
Insgesamt gilt also für die Ableitung
| ∂g |
| ∂wi,j(2) |
Wenn also die Fehlerwerte fj(2) der Schicht 2 bekannt sind, so lassen sich die Gewichte wi,j(1) anpassen. Die Anpassung wird durchgeführt, indem der Gradient mit einem kleinen Faktor α multipliziert wird. Der Faktor α ist die Lernrate.
| ∂g |
| ∂wi,j(1) |
Vektorschreibweise
In Vektorschreibweise ergibt sich die Anpassung dieser Gewichtungen wie folgt:
ΔW = S(1)T · (α · (S(2) – Y) ⊙ S(2) ⊙ (1 – S(2))
Die m(1)×m(2)-Matrix der Gewichtungsänderungen ergibt sich durch Matrixmultiplikation der m(1)×1-Matrix S(1)T (der transponierten 1×m(1)-Matrix S(1)) und einem Ausdruck, der eine 1×m(2)-Matrix darstellt. Dieser Ausdruck enthält eine Multiplikation zwischen dem Skalar α und Vektoren, die komponentenweise miteinander multipliziert werden. Die komponentenweise Multiplikation von Vektoren wird hier mit dem Zeichen ⊙ notiert. Der Vektor 1 – S(2) ergibt sich, indem S(2) komponentenweise von einem Vektor, der aus lauter 1'en besteht, subtrahiert wird.
Anpassung der Gewichtungen zwischen Schicht 0 und Schicht 1
Gegeben ist ein neuronales Netz mit drei Schichten 0, 1, 2. Wie hängt der Fehler fj(2) eines Neurons j in Schicht 2 von einer Gewichtung wk,i(0) von Neuron k in Schicht 0 zu Neuron i in Schicht 1 ab? Die Berechnung erfolgt ganz ähnlich wie die bei der Anpassung der Gewichtungen zwischen Schicht 1 und Schicht 2, ist aber etwas umfangreicher.
- fj(2) hängt von dem Aktivierungspotenzial sj(2) ab
- sj(2) hängt von der Eingabe ej(2) ab
- ej(2) hängt von dem Aktivierungspotenzial si(1) ab
- si(1) hängt von der Eingabe ei(1) ab
- ei(1) hängt vom Gewicht wk,i(0) ab
Somit ergibt sich für die partielle Ableitung von fj(2) nach wk,i(0):
| ∂fj(2) |
| ∂wk,i(0) |
| ∂fj(2) |
| ∂sj(2) |
| ∂sj(2) |
| ∂ej(2) |
| ∂ej(2) |
| ∂si(1) |
| ∂si(1) |
| ∂ei(1) |
| ∂ei(1) |
| ∂wk,i(0) |
Für die einzelnen Ableitungen in der Kette gilt:
| ∂fj(2) |
| ∂sj(2) |
| ∂ |
| ∂sj(2) |
| ∂sj(2) |
| ∂ej(2) |
| ∂ |
| ∂ej(2) |
| ∂ej(2) |
| ∂si(1) |
| ∂ |
| ∂si(1) |
 t st(1)· wt,j(1)eines der t ist gleich i = wi,j(1)
t st(1)· wt,j(1)eines der t ist gleich i = wi,j(1)
| ∂si(1) |
| ∂ei(1) |
| ∂ |
| ∂ei(1) |
| ∂ei(1) |
| ∂wk,i(0) |
| ∂ |
| ∂wk,i(0) |
 t st(0) · wt,i(0)eines der t ist gleich k = sk(0)
t st(0) · wt,i(0)eines der t ist gleich k = sk(0)
Insgesamt gilt also für die Ableitung
| ∂fj(2) |
| ∂wk,i(0) |
Um das Gewicht wk,i(0) in Richtung des Gradienten so anzupassen, dass sich fj(2) verringert, wird
| ∂fj(2) |
| ∂wk,i(0) |
gebildet; hierbei ist α die Lernrate.
Nun beeinflusst wk,i(0) aber alle fj(2) mit j = 0, ..., m(2). Dies bedeutet, dass die Gewichtsänderungen für alle j berechnet und aufsummiert werden müssen, um den Gesamtfehler g zu verringern.
| ∂g |
| ∂wk,i(0) |
 j = 0, ..., m(2)-1 (sj(2) – y) · sj(2) · (1 – sj(2)) · wi,j(1) · si(1) · (1 – si(1)) · sk(0)
j = 0, ..., m(2)-1 (sj(2) – y) · sj(2) · (1 – sj(2)) · wi,j(1) · si(1) · (1 – si(1)) · sk(0)
Etwas umgestellt lautet die Formel
| ∂g |
| ∂wk,i(0) |
 j = 0, ..., m(2)-1 wi,j(1) · (sj(2) – y) · sj(2) · (1 – sj(2))
j = 0, ..., m(2)-1 wi,j(1) · (sj(2) – y) · sj(2) · (1 – sj(2))
In Vektorschreibweise ergibt sich für alle wk,i(0)
Hierbei steht das Zeichen ⊙ wieder für die komponentenweise Multiplikation von Zeilenvektoren gleicher Länge. Das normale Multiplikationszeichen · steht hier für die Matrixmultiplikation, wobei ein Zeilenvektor der Länge m wieder als 1×m-Matrix aufgefasst wird.
In dieser ziemlich komplizierten Formel kommt ein Teil vor, der bereits bei der Anpassung der Gewichte zwischen Schicht 1 und Schicht 2 berechnet worden ist. Dies wird im Backpropagation-Algorithmus ausgenutzt, hier allgemein angegeben für ein neuronales Netz mit n Schichten:
Backpropagation
Eingabe:
Neuronales Netz mit n Schichten, Eingabevektor X, Zielvektor Y, Lernrate α
Methode:
- setze F(r) = H(r+1) · W(r)T
- setze W(r-1) = S(r-1)T · α · H(r)
setze r = n-1
setze F(r) = S(r) – Y
setze H(r) = F(r) ⊙ S(r) ⊙ (1 – S(r))
für r = n-2 abwärts bis 1 wiederhole
setze H(r) = F(r) ⊙ S(r) ⊙ (1 – S(r))
für r = n-1 abwärts bis 1 wiederhole
Die Implementierung in der Programmiersprache Python lautet wie folgt.
y=np.array(y).reshape(1, m[n-1]) # 1 x m[n-1]-Matrix
r=n-1
f[r]=s[r] - y
h[r]=f[r]*s[r]*(1-s[r])
# Fehler zurückpropagieren
for r in range(n-2, 0, -1):
f[r]=np.matmul(h[r+1], w[r].T)
h[r]=f[r]*s[r]*(1-s[r])
# Gewichte anpassen
for r in range(n-1, 0, -1):
w[r-1] -= np.matmul(s[r-1].T, alpha*h[r])
Implementierung der Trainingsphase
Die folgende Funktion training erzeugt mithilfe einer Funktion randomInput verschiedenen Paare (X, Y) von Eingabevektoren X und zugehörigen Zielvektoren Y. Der Eingabevektor wird mit propagate per Vorwärtspropagation im neuronalen Netz verarbeitet. Die Funktion backpropagate vergleicht den errechneten Ausgabevektor mit dem Zielvektor Y und speist den Fehler per Backpropagation zurück in das neuronale Netz, um die Gewichtungen anzupassen. Das Training wird k-mal durchgeführt (zum Beispiel k = 50.000).
for _ in range(k):
x, y=randomInput()
propagate(x)
backpropagate(y)
Anstatt wie hier zufällig erzeugte Daten zu verwenden, wird normalerweise ein Datensatz mit realen Trainingsdaten verwendet, so etwa bei der Erkennung von handgeschriebenen Ziffern.
Anhang: Ableitung der Funktion σ
Es gilt mit zweimaligem Anwenden der Kettenregel, hier ausführlich Schritt für Schritt durchgeführt:
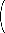
| 1 |
| 1 + e-x |
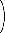 ' = (1 + e-x)-1 'Kettenregel anwenden = (-1) · (1 + e-x)-2 · (1 + e-x)'1 ' = 0 = (-1) · (1 + e-x)-2 · e-x 'Kettenregel anwenden = (-1) · (1 + e-x)-2 · e-x · (-x)'x ' = 1 = (-1) · (1 + e-x)-2 · e-x · (-1) =
' = (1 + e-x)-1 'Kettenregel anwenden = (-1) · (1 + e-x)-2 · (1 + e-x)'1 ' = 0 = (-1) · (1 + e-x)-2 · e-x 'Kettenregel anwenden = (-1) · (1 + e-x)-2 · e-x · (-x)'x ' = 1 = (-1) · (1 + e-x)-2 · e-x · (-1) = | e-x |
| (1 + e-x)2 |
| e-x |
| (1 + e-x)2 |
| 1 |
| (1 + e-x)2 |
| 1 |
| (1 + e-x)2 |
| 1 + e-x |
| (1 + e-x)2 |
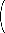
| 1 |
| 1 + e-x |
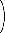 2ersten Bruch kürzen =
2ersten Bruch kürzen = | 1 |
| 1 + e-x |
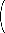
| 1 |
| 1 + e-x |
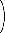 2einsetzen = σ(x) – (σ(x))2ausklammern = σ(x) · (1 – σ(x))
2einsetzen = σ(x) – (σ(x))2ausklammern = σ(x) · (1 – σ(x))
Literatur
[RHW 86] D.E. Rumelhart, G.E. Hinton, R.J. Williams: Learning representations by back-propagating errors. Nature, Vol. 323, 533-536 (1986)
Weiter mit: [Handgeschriebene Ziffern erkennen] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 17.11.2020 Updated: 29.08.2025
Diese Webseiten sind größtenteils während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden