Transformationen
Reduktion eines leichten auf ein schweres Problem
Ein schweres Problem lässt sich nicht auf ein leichtes Problem reduzieren – es sei denn, dass die Schwierigkeit in der Transformation versteckt ist. Denn das schwere Problem ist nicht schwer, wenn es sich auf dem Umweg über das leichte Problem leicht lösen lässt. Dagegen lässt sich ein leichtes Problem ohne Weiteres auf ein schweres Problem "reduzieren". Wir zeigen dies, indem wir das Sortierproblem auf das Travelling Salesman Problem (TSP) reduzieren (Bild 1). Die hier gewählte Transformation ist dieselbe, die auch beim Beweis der unteren Schranke für die Berechnung der konvexen Hülle vorkommt.
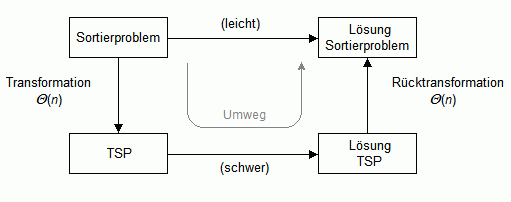
Bild 1: Reduktion des Sortierproblems auf das Travelling-Salesman-Problem (TSP)
Reduktion
Reduktion von SORT auf TSP
Eingabe:
Folge von Zahlen x0, ..., xn-1
Ausgabe:
Die sortierte Folge
Methode:
- Transformation in einen Fall des Travelling-Salesman-Problems:
- Bilde Menge von Punkten pi = (xi, xi2) in der Ebene (Bild 2)
- Berechne xj = min(xi) (in Bild 2 ist j = 4)
- Löse das Travelling-Salesman-Problem:
- Berechne die kürzeste Rundreise mit pj als Startknoten; offensichtlich verläuft die kürzeste Rundreise entlang den Eckpunkten der konvexen Hülle der Punktmenge (rot dargestellt in Bild 2)
- Rücktransformation:
- Bilde die Folge der x-Koordinaten der Knoten der Rundreise; dies ist die sortierte Folge (x4, x3, x1, x0, x5, x2 in Bild 2)
-
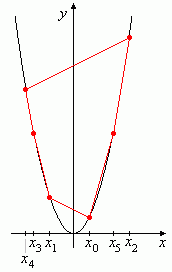
Bild 2:
Durch diese Reduktion ist gleichzeitig bewiesen, dass sich das Travelling-Salesman-Problem nicht schneller als in Ω(n · log(n)) Schritten lösen lässt ;-) Denn ginge es schneller, dann könnte man schneller als in Ω(n · log(n)) Schritten sortieren – dies ist aber nicht möglich, denn Ω(n · log(n)) ist eine untere Schranke für das Sortierproblem.
Weiter mit: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 15.01.2003 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden