Sorting networks

Odd-even mergesort

The odd-even mergesort algorithm was developed by K.E. Batcher [Bat 68]. It is based on a merge algorithm that merges two sorted halves of a sequence to a completely sorted sequence.

In contrast to mergesort, this algorithm is not data-dependent, i.e. the same comparisons are performed regardless of the actual data. Therefore, odd-even mergesort can be implemented as a sorting network.

The following algorithm merges a sequence whose two halves are sorted to a sorted sequence.

Algorithm odd-even merge(n)

Input:

sequence a₀, ..., a_n-1 of length n > 1 whose two halves a₀, ..., a_n/2-1 and a_n/2, ..., a_n-1 are sorted (n a power of 2)

Output:

the sorted sequence

Method:

if n > 2 then

apply odd-even merge(n/2) recursively to the even subsequence a₀, a₂, ..., a_n-2 and to the odd subsequence a₁, a₃, , ..., a_n-1
comparison [i:i+1] for all i ∈ {1, 3, 5, 7, ..., n-3}

else

comparison [0:1]

The correctness of the merge algorithm is proved using induction and the 0-1-principle.

If n = 2¹ the sequence is sorted by the comparison [0:1]. So let n = 2^k, k > 1 and assume the algorithm is correct for all smaller k (induction hypothesis).

Consider the 0-1-sequence a = a₀, ..., a_n-1 to be arranged in rows of an array with two columns. The corresponding mapping of the index positions is shown in Figure 1a, here for n = 16. Then Figure 1b shows a possible situation with a 0-1-sequence. Each of its two sorted halves starts with some 0's (white) and ends with some 1's (gray).

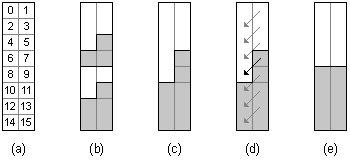
Figure 1: Situations during execution of odd-even merge

In the left column the even subsequence is found, i.e. all a_i with i even, namely a₀, a₂, a₄ etc.; in the right column the odd subsequence is found, i.e. all a_i with i odd, namely a₁, a₃, a₅ etc. Just like the original sequence the even as well as the odd subsequence consists of two sorted halves.

By induction hypothesis, the left and the right column are sorted by recursive application of odd-even merge(n/2) in step 1 of the algorithm. The right column can have at most two more 1's than the left column (Figure 1c).

After performing the comparisons of step 2 of the algorithm (Figure 1d), in each case the array is sorted (Figure 1e).

Let T(n) be the number of comparisons performed by odd-even merge(n). Then we have for n > 2

T(n) = 2·T(n/2) + n/2-1.

With T(2) = 1 we have

T(n) = n/2 · (log(n)-1) + 1 ∈ O(n·log(n)).

By recursive application of the merge algorithm the sorting algorithm odd-even mergesort is formed.

Algorithm odd-even mergesort(n)

Input:

sequence a₀, ..., a_n-1 (n a power of 2)

Output:

the sorted sequence

Method:

if n > 1 then

apply odd-even mergesort(n/2) recursively to the two halves a₀, ..., a_n/2-1 and a_n/2, ..., a_n-1 of the sequence
odd-even merge(n)

Figure 2 shows the odd-even mergesort network for n = 8.

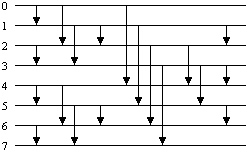
Figure 2: Odd-even mergesort for n = 8

The number of comparators of odd-even mergesort is in O(n log(n)²).

An implementation of odd-even mergesort in Java is given in the following. The algorithm is encapsulated in a class OddEvenMergeSorter. Its method sort passes the array to be sorted to array a and calls function oddEvenMergeSort.

Function oddEvenMergeSort recursively sorts the two halves of the array. Then it merges the two halves with oddEvenMerge.

Function oddEvenMerge picks every 2r-th element starting from position lo and lo+r, respectively, thus forming the even and the odd subsequence. According to the recursion depth r is 1, 2, 4, 8, ....

With the statements

Sorter s=new OddEvenMergeSorter();
s.sort(b);

an object of type OddEvenMergeSorter is created and its method sort is called in order to sort array b. The length n of the array must be a power of 2.

public class OddEvenMergeSorter implements Sorter
{
    private int[] a;

    public void sort(int[] a)
    {
        this.a=a;
        oddEvenMergeSort(0, a.length);
    }

    /** sorts a piece of length n of the array
     *  starting at position lo
     */
    private void oddEvenMergeSort(int lo, int n)
    {
        if (n>1)
        {
            int m=n/2;
            oddEvenMergeSort(lo, m);
            oddEvenMergeSort(lo+m, m);
            oddEvenMerge(lo, n, 1);
        }
    }

    /** lo is the starting position and
     *  n is the length of the piece to be merged,
     *  r is the distance of the elements to be compared
     */
    private void oddEvenMerge(int lo, int n, int r)
    {
        int m=r*2;
        if (m<n)
        {
            oddEvenMerge(lo, n, m);      // even subsequence
            oddEvenMerge(lo+r, n, m);    // odd subsequence
            for (int i=lo+r; i+r<lo+n; i+=m)
                compare(i, i+r);
        }
        else
            compare(lo, lo+r);
    }

    private void compare(int i, int j)
    {
        if (a[i]>a[j])
            exchange(i, j);
    }

    private void exchange(int i, int j)
    {
        int t=a[i];
        a[i]=a[j];
        a[j]=t;
    }

}    // end class OddEvenMergeSorter

There are other sorting networks that have a complexity of O(n log(n)²), too, e.g. bitonic sort and shellsort. However, odd-even mergesort requires the fewest comparators of these. The following table shows the number of comparators for n = 4, 16, 64, 256 and 1024.

`n`	odd-even mergesort	bitonic sort	shellsort
4	5	6	6
16	63	80	83
64	543	672	724
256	3839	4608	5106
1024	24063	28160	31915

Exercise 1: Give the exact formula for T(n), the number of comparators of odd-even mergesort. Check your formula by comparing its results with the entries in the table above.

[Bat 68] K.E. Batcher: Sorting Networks and their Applications. Proc. AFIPS Spring Joint Comput. Conf., Vol. 32, 307-314 (1968)

[Sed 03] R. Sedgewick: Algorithms in Java, Parts 1-4. 3rd edition, Addison-Wesley (2003)

Next: [Bitonic sort] or [up]

H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 31.01.1998 Updated: 07.02.2023

Sorting networks

Odd-even mergesort

Merge algorithm

Correctness

Analysis

Sorting algorithm

Program

Conclusions

References