Algorithmen der linearen Algebra
Gram-Schmidt-Verfahren
Das Gram-Schmidt-Verfahren wandelt eine beliebige Basis eines euklidischen Vektorraums in eine orthogonale Basis um. Ein euklidischer Vektorraum ist ein endlichdimensionaler Vektorraum, in welchem ein Skalarprodukt definiert ist.
Grundlagen
Definition: Sei V ein Vektorraum über einem Körper K. Eine Menge von Vektoren X = {x0, ..., xm-1} heißt linear unabhängig, wenn sich der Nullvektor nur auf triviale Weise als Linearkombination der xi mit Koeffizienten ki aus dem Körper K darstellen lässt. Dies bedeutet, dass
k0·x0 + k1·x1 + ... + km-1·xm-1 = 0
nur dann möglich ist, wenn alle Koeffizienten ki = 0 sind.
Sei X = {x0, ..., xm-1} eine Menge von linear unabhängigen Vektoren. Die Menge aller Linearkombinationen
U = { k0·x0 + k1·x1 + ... + km-1·xm-1 | ki ∈ K }
bildet einen Unterraum U des Vektorraums V. Die Menge X ist eine Basis des Unterraums U. Die Anzahl m der Basisvektoren xi wird als die Dimension des Unterraums U bezeichnet.
Jede beliebige Menge von m linear unabhängigen Vektoren aus U kann als Basis für U dienen. Oft ist es jedoch vorteilhaft, wenn die Basisvektoren paarweise orthogonal zueinander sind, also "senkrecht aufeinander stehen".
Orthogonalität
Definition: Zwei Vektoren u und v sind orthogonal zueinander, wenn ihr Skalarprodukt gleich Null ist, wenn also gilt
u·v = 0
Es gibt unterschiedliche Schreibweisen für das Skalarprodukt von zwei Vektoren u und v, neben u·v auch (u,v) oder ⟨u,v⟩.
Orthogonale Vektoren im Raum ℝ2 stehen senkrecht aufeinander. Dies bietet eine gute Anschauung für Orthogonalität. Der Begriff der Orthogonalität gilt aber in jedem Vektorraum, in welchem ein Skalarprodukt definiert ist.
Anschaulich anhand von Vektoren im Raum ℝ2 lässt sich auch die orthogonale Projektion u' eines Vektors v auf einen Vektor u darstellen (Bild 1).
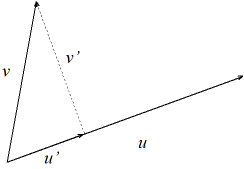
Bild 1: Orthogonale Projektion des Vektors v auf den Vektor u
Die Berechnung der orthogonalen Projektion basiert wiederum nur auf dem Skalarprodukt, sodass sie in jedem Vektorraum durchgeführt werden kann, in welchem ein Skalarprodukt definiert ist, auch wenn dort die Anschauung nicht in dieser Weise gegeben ist.
| u·v |
| u·u |
Der gestrichelt gezeichnete Vektor v' in Bild 1 ergibt sich als
v' = -u' + v = v – u'
Der Vektor v' steht senkrecht auf dem Vektor u.
Wenn u und v die Basisvektoren eines Unterraums U sind, so lassen sich aus ihnen auf diese Weise zwei orthogonale Basisvektoren u und v' konstruieren. Da v' eine Linearkombination von u und v ist, erzeugen die orthogonalen Basisvektoren denselben Unterraum U.
Verfahren
Auf dieser Konstruktion beruht das Gram-Schmidt-Verfahren, das eine beliebige Basis B eines Vektorraums in eine Basis aus paarweise orthogonalen Vektoren umformt.
Die folgende Funktion gramSchmidt übernimmt als Parameter einen Verweis auf eine Matrix b, deren Zeilen die Basisvektoren sind. Die Basisvektoren sind Vektoren des ℝn, bestehend also aus Kommazahlen.
Im Verlauf der Berechnung werden die m Basisvektoren einer nach dem anderen in zueinander orthogonale Basisvektoren umgeformt. Am Ende besteht b aus m orthogonalen Basisvektoren.
Das Programm verwendet die Bibliothek numpy, die ein einfaches Rechnen mit Vektoren ermöglicht. Die Funktion dot berechnet das Skalarprodukt. Im Hauptprogramm wird mit der Funktion array eine Matrix im numpy-Format erzeugt.
# formt eine Matrix aus Basisvektoren in eine Matrix aus
# orthogonalen Basisvektoren um
def gramSchmidt(b):
bb=[]
m=len(b) # Anzahl der Basisvektoren
for i in range(m):
for j in range(i):
b[i]-=np.dot(b[j],b[i])/bb[j]*b[j]
bb+=[np.dot(b[i],b[i])]
# Hauptprogramm
u=np.array([[2,0], [1,1]], dtype="double")
print(u)
print()
gramSchmidt(u)
print(u)
print()
In diesem einfachen Beispiel wird eine Matrix bestehend aus den zwei Basisvektoren [2,0] und [1,1] in eine Matrix bestehend aus den zwei orthogonalen Basisvektoren [2,0] und [0,1] umgeformt.
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 22.04.2021 Updated: 12.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden