Mathematische Grundlagen
Quaternionen
Erstmals beschrieben wurden Quaternionen 1853 von W. R. Hamilton
, heute finden sie Anwendung in der Computergrafik.
Definition: Eine Quaternion ist ein Quadrupel q = (a, b, c, d) mit a, b, c, d ∈ ℝ. Die Menge der Quaternionen wird mit ℍ bezeichnet.
In ℍ sind in bestimmter Weise eine Addition und eine Multiplikation definiert. Addition und Multiplikation in ℍ lassen sich auf die Addition bzw. Multiplikation von reellen Zahlen zurückführen.
Eine Möglichkeit hierzu ist, Quaternionen als hyperkomplexe Zahlen aufzufassen (mit 3 Imaginärteilen). Einer Quaternion (a, b, c, d) entspricht dann der Term
a + bi + cj + dk
Hierbei sind i, j und k drei unterschiedliche Arten von imaginären Zahlen. Addition und Multiplikation von Quaternionen ergeben sich nun durch Anwendung der Rechenregeln für Terme reeller Zahlen, wobei für die Multiplikation von i, j und k folgende Verknüpfungstafel zugrunde gelegt wird:
| · | i | j | k |
|---|---|---|---|
| i | -1 | k | -j |
| j | -k | -1 | i |
| k | j | -i | -1 |
Wie aus der Verknüpfungstafel ersichtlich, ist die Multiplikation nicht kommutativ, denn es ist z.B. i·j = k, aber j·i = -k.
Satz: Die Menge der Quaternionen (ℍ, +, ·) bildet einen Schiefkörper.
Quaternionen lassen sich auch als 2×2-Matrizen komplexer Zahlen oder 4×4-Matrizen reeller Zahlen auffassen. Mit den Verknüpfungen Matrixaddition und Matrixmultiplikation ergibt sich derselbe Schiefkörper.
Einer Quaternion (a, b, c, d) entspricht hierbei die komplexe 2×2-Matrix
 |
|  |
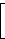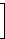bzw. die reelle 4×4-Matrix
 |
|  |
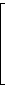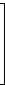Definition: Die zu einer Quaternion q = (a, b, c, d) konjugierte Quaternion ist
q = (a, -b, -c, -d)
Der Betrag von q ist definiert als
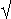q·q = 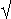a2 + b2 + c2 + d2
Behauptung: Die zu einer Quaternion q multiplikativ inverse Quaternion ist
| q |
| |q|2 |
Beweis: Es ist
| q·q |
| |q|2 |
| q·q |
| q·q |
Als unmittelbare Folgerung ergibt sich, dass für eine Quaternion q mit dem Betrag 1 gilt: q-1 = q.
Berechnung von Rotationen mit Quaternionen
Eine Rotation um die x-Achse um einen Winkel α wird durch die Quaternion q = (cos(α/2), sin(α/2), 0, 0) repräsentiert. Ein Punkt P = (x0, y0, z0) wird durch die Quaternion p = (0, x0, y0, z0) repräsentiert. Der rotierte Punkt p° ergibt sich als
p° = q · p · q
Die Rotation um einen beliebigen normierten Vektor (x, y, z) um einen Winkel α wird durch die Quaternion
q = (cos(α/2), x·sin(α/2), y·sin(α/2), z·sin(α/2))
repräsentiert.
Tatsächlich repräsentiert jede Quaternion mit dem Betrag 1 eine Rotation. Die Menge der so repräsentierten Rotationen bildet also die Oberfläche einer Einheitskugel im ℝ4. Zwischen zwei Rotationen lässt sich interpolieren, indem zwischen zwei Punkten auf der Kugeloberfläche interpoliert wird.
Literatur
[TL 94] K.D. Tönnies, H.U. Lemke: 3D-Computergrafische Darstellungen. Oldenbourg (1994)
Weiter: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 22.08.2000 Updated: 10.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden