Systematische Programmentwicklung
Korrektheit von If-Else-Anweisungen
Die Schlussregel für die If-Else-Anweisung ergibt sich aus dem Flussdiagramm (Bild 1). Sie lautet
| {P ∧ B} S1 {Q}, {P ∧ ¬B} S2 {Q} |
| {P} if(B) S1 else S2 {Q} |
Um den Beweis für {P} if(B) S1 else S2 {Q} zu erhalten, beweisen Sie die Prämissen If1 und If2:
- If1: {P ∧ B} S1 {Q}
- If2: {P ∧ ¬B} S2 {Q}
In Bild 1 erkennen Sie diese Vor- und Nachbedingungen im Flussdiagramm der If-Else-Anweisung.
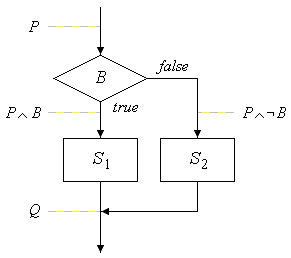
Bild 1: Vor- und Nachbedingungen bei der If-Else-Anweisung
Beispiel: Mit dem folgenden Programm berechnen Sie das Maximum von zwei Werten a und b, als Ergebnis erhalten Sie m.
m=a;
else
m=b;
Die Nachbedingung Q des Programms ist
Q: m = max(a, b)
Sie führen nun zwei getrennte Beweise für die beiden Prämissen, und zwar zunächst {P ∧ B} m=a; {Q} und dann {P ∧ ¬B} m=b; {Q} mit
B: a > b
Prämisse If1: If-Teil
Zuerst zeigen Sie {P ∧ B} m=a; {Q}.
Der Beweis wird von unten nach oben geführt, unter Benutzung der Wertzuweisungsregel und der Konsequenzregel. Es stellt sich heraus, dass P: true die schwächste Vorbedingung für diesen Zweig ist.
| { P ∧ B } | (8) | |
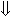 | { true ∧ a > b } | (7) |
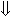 | { a > b } | (6) |
| { a > b ∨ a = b } | (5) | |
| { a ≥ b } | (4) | |
| { a = max(a, b) } | (3) | |
| m=a; | ||
| { m = max(a, b) } | (2) | |
| { Q } | (1) |
Die Konsequenzregel ermöglicht das Verschärfen von Bedingungen nach oben hin. Beim Übergang von Schritt (5) zu Schritt (6) machen Sie davon Gebrauch, indem Sie die Bedingung durch Weglassen einer Oder-Bedingung verschärfen. Beim Übergang von Schritt (6) zu Schritt (7) verschärfen Sie die Bedingung durch Hinzufügen einer Und-Bedingung 1).
Prämisse If2: Else-Teil
Als nächstes zeigen Sie {P ∧ ¬B} m=b; {Q}.
Auch hier ergibt sich P: true als schwächste Vorbedingung.
| { P ∧ ¬B } | (8) | |
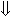 | { true ∧ ¬ a > b } | (7) |
| { ¬ a > b } | (6) | |
| { a ≤ b } | (5) | |
| { b ≥ a } | (4) | |
| { b = max(a, b) } | (3) | |
| m=b; | ||
| { m = max(a, b) } | (2) | |
| { Q } | (1) |
Nachdem Sie diese beiden Beweise getrennt geführt haben, können Sie aufgrund der Schlussregel für die If-Anweisung folgern
{ true } if (a>b) m=a; else m=b; { m = max (a, b) }
d.h. Sie haben bewiesen, dass ohne irgendeine besondere Vorbedingung (außer der Bedingung true, die immer wahr ist) das Programm das Gewünschte tut.
1) nur formal, nicht tatsächlich, denn (6) und (7) sind äquivalent
H.W. Lang mail@hwlang.de Impressum Datenschutz
Diese Webseiten sind größtenteils während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden