Theoretische Informatik
Syntaxdiagramm
Ein regulärer Ausdruck lässt sich sehr einfach in ein Syntaxdiagramm überführen. Das Syntaxdiagramm beschreibt die reguläre Sprache, die von dem regulären Ausdruck erzeugt wird, indem es in anschaulicher Weise zeigt, welche Wörter gebildet werden können.
Beispiel: Der reguläre Ausdruck R = a | a(a|b)*a wird in folgendes Syntaxdiagramm überführt (Bild 1):
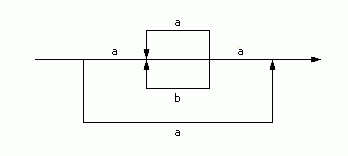
Bild 1: Syntaxdiagramm für den regulären Ausdruck a | a(a|b)*a
Das Diagramm wird von links beginnend in Pfeilrichtung bis zum Ausgang durchlaufen. Dabei werden die Alphabetzeichen, die an den durchlaufenen Pfeilen stehen, zu einem Wort aneinandergereiht. Jeder mögliche Pfad durch das Diagramm, der vom Eingang bis zum Ausgang verläuft, entspricht auf diese Weise einem Wort der Sprache, die von dem regulären Ausdruck R erzeugt wird.
Wird beispielsweise das Diagramm geradeaus von links nach rechts durchlaufen, so wird das Wort aa gebildet. Wird unterwegs einmal die Schleife mit dem b durchlaufen, ergibt sich das Wort aba. Für das Wort a wird der große Umweg unten herum gewählt.
Es gibt zwei Sichtweisen, wie ein Syntaxdiagramm eine Sprache definiert: indem es Wörter der Sprache erzeugt, oder indem es Wörter der Sprache erkennt. Im ersten Fall beginnen wir mit einem leeren Wort und hängen beim Durchlaufen des Syntaxdiagramms Zeichen um Zeichen an, im anderen Fall liegt uns ein Wort vor und wir arbeiten es zeichenweise ab, während wir das Syntaxdiagramm durchlaufen.
In beiden Fällen ist das Durchlaufen eines Syntaxdiagramms im Allgemeinen ein nichtdeterministischer Vorgang. Wenn wir an Verzweigungspunkte des Diagramms gelangen, haben wir die Wahl, in welche Richtung wir abbiegen. Gelegentlich müssen wir die richtige Wahl sozusagen mit schlafwandlerischer Sicherheit treffen. Um beispielsweise das Wort aaa zu erzeugen bzw. zu erkennen, müssen wir im Syntaxdiagramm an der ersten Verzweigung geradeaus gehen, an der nächsten Verzweigung nach oben abbiegen und einmal in der a-Schleife kreisen, und beim nächsten Mal an dieser Verzweigung geradeaus zum Ausgang gehen. Biegen wir falsch ab, gelingt es uns nicht, das Wort aaa zu erzeugen bzw. zu erkennen.
Ein Syntaxdiagramm besagt also im Allgemeinen nicht, wie ein bestimmtes Wort erzeugt oder erkannt wird, sondern nur ob es prinzipiell erzeugt oder erkannt werden kann.
Wörter allerdings, die nicht zu der Sprache gehören, die durch das Syntaxdiagramm definiert ist, lassen sich auf keine Weise beim Durchlaufen des Syntaxdiagramms erzeugen bzw. erkennen.
In obigem Beispiel lässt sich etwa das Wort abb nicht erzeugen. Denn es gibt keinen Pfad durch das Syntaxdiagramm, der diesem Wort entspricht. Beim Versuch das Wort abb zu erkennen, erreichen wir zwar mit a die Schleife, die mit b markiert ist, durchlaufen diese zweimal, aber kommen dann nicht weiter bis zum Ausgang des Syntaxdiagramms.
Syntax von Programmiersprachen
Die Syntax von Programmiersprachen wurde schon sehr früh in Form von Syntaxdiagrammen angegeben. Als einfachstes Beispiel zeigt Bild 2 das Syntaxdiagramm für identifier in der Programmiersprache Pascal, wie es im Pascal User Manual and Report von 1975 angegeben ist [JW 75]. Durch das Syntaxdiagramm wird festgelegt, wie identifier, also Bezeichner für Programmvariablen oder Funktionen gebildet werden: Ein Bezeichner fängt mit einem Buchstaben (letter) an und geht dann mit beliebig vielen Buchstaben (letter) oder Ziffern (digit) weiter. Im Unterschied zu unserer Darstellung von Syntaxdiagrammen sind in den Pascal-Syntaxdiagrammen die Beschriftungen der Pfeile nicht darüber oder darunter angebracht, sondern in Form von Ovalen oder Kästchen in die Pfeile eingebettet.
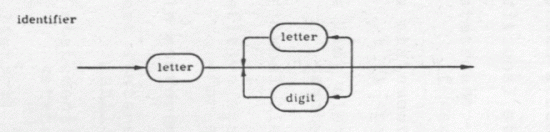
Bild 2: Syntaxdiagramm für identifier in der Programmiersprache Pascal
Mögliche Bezeichner sind also
x, x34, counter, getNext, uv2wx2y.
Keine Bezeichner dagegen sind
3n, next-state, my Text, a.next,
da diese Zeichenketten mit einer Ziffer anfangen oder Zeichen enthalten, die keine Buchstaben oder Ziffern sind.
Weitere Ausdruckskraft erlangen Syntaxdiagramme, wenn sie Kästchen enthalten, die als Platzhalter wiederum für andere Syntaxdiagramme stehen. Hiervon wird später die Rede sein; zunächst erlauben wir dies nicht.
Syntaxdiagramm als Brettspiel
Wir verändern Syntaxdiagramme nun geringfügig in einer bestimmten Weise. Am Anfang des Syntaxdiagramms führen wir ein Startfeld ein, am Ende ein Endfeld, und an den Knotenpunkten des Syntaxdiagramms führen wir quasi als Zwischenstationen weitere Felder ein.
Beispiel: Das folgende Bild 3 zeigt das entsprechend umgestaltete Syntaxdiagramm aus dem vorangegangenen Beispiel. Am Eingang und am Ausgang sowie an den Knotenpunkten des Syntaxdiagramms sind Felder eingeführt worden, dargestellt durch Kreise. Das Startfeld ist durch einen "aus dem Nichts kommenden" Pfeil markiert, das Endfeld durch einen doppelten Kreis. Alle anderen Felder sind Zwischenstationen.
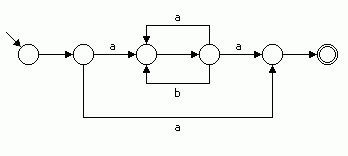
Bild 3: Syntaxdiagramm mit eingeführten Zwischenstationen
Ein so umgestaltetes Syntaxdiagramm lässt sich als eine Art Brettspiel verwenden. Auf die Felder können wir eine Spielfigur, zum Beispiel ein "Mensch-ärgere-dich-nicht"-Männchen, setzen. Wir beginnen beim Startfeld, ziehen mit der Spielfigur entlang der Pfeile von Feld zu Feld und reihen dabei die Zeichen, die uns begegnen, aneinander. Das Spiel ist "gewonnen", wenn es gelingt, vom Startfeld bis zum Endfeld zu ziehen und dabei ein vorgegebenes Wort wie etwa abba zu erzeugen bzw. zu erkennen, je nach Sichtweise.
Beispiel: Im oben abgebildeten Spiel ziehen wir vom Startfeld zunächst drei Felder geradeaus. Dabei begegnet uns das Zeichen a. Dann kreisen wir zweimal entlang der unteren Schleife, dabei begegnen uns zwei b's. Zum Schluss ziehen wir zwei Felder geradeaus bis zum Endfeld; dabei begegnet uns ein a. Auf diese Weise haben wir das Wort abba erzeugt bzw. erkannt.
Das Wort abb dagegen können wir nicht erzeugen bzw. erkennen, weil wir damit nicht zum Endfeld durchkommen.
Wir werden später das Brettspiel noch so verändern, dass wir mit der Spielfigur nicht mehr intuitiv richtig ziehen müssen, um zum Endfeld zu gelangen. Stattdessen spielen wir alle Zugmöglichkeiten parallel durch, indem wir mehrere Spielfiguren verwenden.
Zusammenhang mit nichtdeterministischen endlichen Automaten
Wie wir im nächsten Abschnitt sehen werden, ist ein so erstelltes Brettspiel nichts anderes als der Zustandsgraph eines nichtdeterministischen endlichen Automaten. Die Felder sind die Zustände des Automaten, die Pfeile sind entsprechende Zustandsübergänge. Es treten auch Zustandsübergänge auf, die mit keinem Zeichen markiert sind. Diese Zustandsübergänge stellen sogenannte Epsilon-Übergänge dar. Der entsprechende Automat ist also ein nichtdeterministischer endlicher Automat mit Epsilon-Übergängen.
Literatur
[JW 75] K. Jensen, N. Wirth: Pascal User Manual and Report. 2. Auflage, Springer (1975)
Weiter mit: [Nichtdeterministischer endlicher Automat] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 20.01.2011 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden