A Characterization of the Chomsky Hierarchy
by String Turing Machines
Hans Werner Lang
Flensburg University of Applied Sciences
A string Turing machine is a variant of a standard Turing machine designed for easy manipulation of strings. In contrast to the standard Turing machine which can only move left (L) and right (R) on its tape, a string Turing machine can also insert (I) and delete (D) symbols in its string. It is easy to see that the models of standard and string Turing machines are equivalent in computing power. However, in case of the string Turing machine, imposing restrictions on the allowed cursor actions {I, L, R, D} of the machine exactly yield recognizers for the type-i language classes of the Chomsky hierarchy [Lan 10].
| Language class | Cursor actions |
|---|---|
| Type 0 | I, L, R, D |
| Type 1 | L, R, D |
| Type 2 | R, D |
| Type 3 | D |
Figure 1: Allowed cursor actions of string Turing machines
In the following, the Chomsky hierarchy of language classes as characterized by certain restricted forms of grammars is revisited. Then, the new characterization by certain restrictions of string Turing machines is introduced.
Chomsky hierarchy
The Chomsky hierarchy identifies language classes ℒ0, ℒ1, ℒ2, ℒ3 where
ℒ0 ⊃ ℒ1 ⊃ ℒ2 ⊃ ℒ3
All the inclusions are proper. The language classes are denoted as type-i languages for i = 0, 1, 2, 3.
ℒ1 is also denoted as the class of context-sensitive languages, ℒ2 as the class of context-free languages, and ℒ3 as the class of regular languages, because their languages are generated by context-sensitive, context-free, and regular grammars, respectively.
Grammars
Languages can be generated by grammars.
Definition: A grammar is a tuple
G = (V, T, P, S)
with
| V | the alphabet of variables or nonterminal symbols, | |
| T | the alphabet of terminal symbols where V ∩ T = ∅; moreover, let A = V ∪ T, | |
| P ⊆ A+ × A* | a finite relation; the elements of P are called productions or replacement rules, | |
| S ∈ V | a special variable, the start symbol. |
The replacement rules are written in the form u → v, indicating that the subword u occurring in some word w may be replaced by the subword v. Given a grammar, the words of a language are generated by applying such a sequence of replacements to the start symbol until a word consisting of terminal symbols only is reached. The sequence of replacements is called a derivation of the word.
Languages can also be recognized by grammars in the sense that all words that can be reduced to the start symbol belong to the language [Sal 73]. Such a reduction is a derivation in opposite direction. The string Turing machine described later makes use of reductions.
Special grammars
Certain restrictions to the form of the productions of a grammar may or may not restrict its power to generate a language. However, the restriction that
P ⊆ V × A*
requiring that the left side of each production consists of exactly one variable restricts the languages generated by this kind of grammars to the class ℒ2 which is a proper subset of ℒ0.
It turns out that the following restrictions imposed on the form of the productions of a grammar correspond to the language classes of the Chomsky hierarchy [Sal 73].
| Type | Productions of the form | Language class | Name |
|---|---|---|---|
| 0 | u → v | ℒ0 | Recursively enumerable languages |
| 1 | u → v with |u| ≤ |v| | ℒ1 | Context-sensitive languages |
| 2 | X → v | ℒ1 | Context-free languages |
| 3 | X → aY or X → a | ℒ3 | Regular languages |
where u ∈ A+, v ∈ A*, X, Y ∈ V, a ∈ T.
If necessary, as an exception the production S → ε is allowed to produce the empty word ε.
String Turing machine
A string Turing machine is a device as shown in Figure 2. It has access to the symbols of a string, one at a time. A cursor points to the current position. The machine can read the symbol at the cursor position (the cursor symbol) and it can overwrite that symbol by some other symbol. It can also move the cursor to the left and to the right. Moreover, a string Turing machine can insert a symbol at the cursor position and it can delete the cursor symbol.

Figure 2: String Turing machine
Initially, the string consists of an input word enclosed by the special delimiter symbols $ and &. The string has finite length, however, by inserting symbols, it can be made arbitrarily long.
The insert action is performed as depicted in Figure 3(a). The prefix of the string including the cursor symbol is moved one position to the left. A blank symbol is inserted and becomes the new cursor symbol. The delete action is shown in Figure 3(b). The cursor symbol is deleted. The prefix of the string left to the cursor is moved one position to the right. Its last symbol becomes the new cursor symbol.
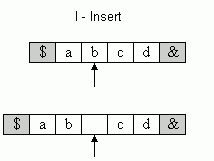

Figure 3: (a) Insert and (b) delete action
Formally, a string Turing machine is defined as follows.
Definition: A nondeterministic string Turing machine is a tuple
M = (Z, E, A, d, q, p)
with
| Z | a finite, non-empty set of states, | |
| E | the input alphabet, | |
| A | the string alphabet where E ⊆ A, | |
| d | the transition relation with d ⊆ Z × A × A' × Z where A' = A ∪ {L, R, I, D}, | |
| q ∈ Z | the start state, | |
| p ∈ {$, &} | the start position. |
The string alphabet A contains the special symbols $, & and the blank symbol  ; these symbols do not belong to the input alphabet. The elements of the set {L, R, I, D} do not belong to A, these elements are called cursor actions.
; these symbols do not belong to the input alphabet. The elements of the set {L, R, I, D} do not belong to A, these elements are called cursor actions.
At the beginning, the string Turing machine is in its start state and the cursor points either to symbol $ or to symbol &.
An element (s, a, a', s') of the transition relation is interpreted in the following way. If the string Turing machine is in state s and reads symbol a at the cursor position, it replaces symbol a by symbol a' and enters state s'. However, if a' is not a symbol but one of the cursor actions, the string Turing machine does not overwrite symbol a but performs the corresponding cursor action: move left (L), move right (R), insert (I) or delete (D).
The string Turing machine accepts an input word w, if there is a sequence of transitions that deletes its string completely.
Equivalence with standard Turing machine
A standard Turing machine can simulate a string Turing machine. The standard Turing machine uses as tape alphabet the alphabet A of the string Turing machine plus symbols a' for all symbols a in A.
It then simulates the insert action as follows. It overwrites the symbol a under its read/write head by the symbol a'. Then it moves all symbols to the right of symbol a' by one position to the right. It returns to symbol a', overwrites it by a, moves one position to the right and prints a blank symbol.
In a similar way, the standard Turing machine simulates the delete action. All other actions are identical to those of the string Turing machine.
The standard Turing machine enters the accepting state when it has deleted all symbols on the tape.
A string Turing machine can simulate a standard Turing machine. It performs identical actions as the standard Turing machine, except when it reaches the delimiter symbols $ or & (which do not belong to the tape alphabet of the standard Turing machine simulated). Then it performs insert actions if it needs space.
When the standard Turing machine enters an accepting state and stops, the string Turing machine deletes its string so that it accepts, too. Otherwise, the string Turing machine does not accept, because at least the symbols $ and & remain.
Recognition of languages by string Turing machines
Given a grammar G and a nonempty word w as input string, the string Turing machine tries to reduce the word w to the start symbol S of the grammar. It does so by replacing the right side of some production that occurs in w by the corresponding left side in a nondeterministic way. It repeats this procedure until only the start symbol S remains. Finally, it deletes S and the delimiter symbols $ and & and recognizes the word w. Otherwise, if no such reduction sequence to the start symbol S is possible, it does not recognize the word w.
The following example illustrates the way a word is recognized by a string Turing machine.
Example 1: Consider the grammar
| S | 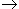 | Ab | ASb |
| A | 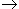 | a |
and let w = aabb be the input word.
The string Turing machine first reduces each a to A by the production A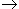 a yielding the string AAbb. When it reads the first b it chooses production S
a yielding the string AAbb. When it reads the first b it chooses production S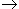 Ab. It deletes b with the result that A appears at the cursor position. It overwrites A by the left side of the production, S, yielding the string ASb. It then moves the cursor to the right, reads b, and applies the production S
Ab. It deletes b with the result that A appears at the cursor position. It overwrites A by the left side of the production, S, yielding the string ASb. It then moves the cursor to the right, reads b, and applies the production S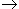 ASb. Namely, it deletes b, deletes S, and overwrites A by the left side S. Now it has reduced the input word w to the start symbol S. In order to make sure that the current word is just S, it moves the cursor to the right, deletes the delimiter symbol &, deletes S, and deletes the other delimiter symbol $. Since the string is now empty, the string Turing machine accepts the input word.
ASb. Namely, it deletes b, deletes S, and overwrites A by the left side S. Now it has reduced the input word w to the start symbol S. In order to make sure that the current word is just S, it moves the cursor to the right, deletes the delimiter symbol &, deletes S, and deletes the other delimiter symbol $. Since the string is now empty, the string Turing machine accepts the input word.
The following simulation shows the behavior of the string Turing machine of this example.
Restriction of cursor actions
When the right side of a production is longer than the left side, the string Turing machine needs to perform delete actions. When the right side is shorter than the left side, it needs to perform insert actions. However, this last case does only occur in proper type-0 grammars. Thus, any type-1 language is recognizable by a string Turing machine without insert actions.
This observation is part of the following hierarchy theorem for string Turing machines. Recall that the cursor actions L, R, I, D denote left move, right move, insert and delete, respectively.
Theorem:
Any type-0 language is recognizable by a string Turing machine with cursor actions {L, R, I, D}.
Any type-1 language is recognizable by a string Turing machine with cursor actions {L, R, D}.
Any type-2 language is recognizable by a string Turing machine with cursor actions {R, D}.
Any type-3 language is recognizable by a string Turing machine with cursor actions {D}.
Proof sketch:
The string Turing machine recognizes a word w of a type-0 language by nondeterministic application of reduction steps until the start symbol S of the grammar is reached, and by finally deleting $S&.
In the same way, a string Turing machine recognizes a word w of a type-1 language. However, every type-1 language has a monotonic grammar, i.e. a grammar where no right side of a production is shorter than the left side. Thus, each reduction step can be performed without insert actions.
Recognition of a type-2 or context-free language is performed essentially in the same way. However, since every word w of a context free language has a derivation tree, reduction of w to the start symbol S is done as follows. Whenever the symbol read belongs to a rightmost branch in the derivation tree, the corresponding production is applied. This is done by performing delete actions for all symbols of the right side of the production except of the last symbol, which is overwritten by the left side of the production. When the symbol read does not belong to a rightmost branch, a move right action is performed. Thus, no move left actions are necessary.
In this way, the string Turing machine simulates a pushdown automaton. The prefix of the string including the cursor position corresponds to the stack of the pushdown automaton.
Since the string Turing machine does not know the derivation tree, it acts nondeterministically. Basically, it applies reduction steps as soon as possible, but there may be cases where the correct reduction step cannot be chosen deterministically.
The simplest reduction process occurs when the grammar is in reverse Greibach normal form, as in Example 1. Then after each move right action a reduction step takes place. However, also in this case different reduction steps may be possible.
Every type-3 language is generated by a left linear grammar. A string Turing machine with cursor actions {D} starts at the delimiter symbol & and reads and deletes the input word from right to left. When reading the first symbol a, it applies some production X → a and enters state X. Then it reads the next symbol b and applies some production Y → Xb and enters state Y, and so on. If it reads the delimiter symbol $ while being in the state of the start symbol S, it deletes $ and accepts, otherwise it overwrites $ with $ and rejects (see Example 2).
It may seem strange that in the case of type-3 languages the string Turing machine processes the input word from right to left. However, if acceptance by empty string is required there is no other choice. Another possibility would have been to define acceptance by final state and to restrict the type-3 cursor actions to {R}.
Examples of string Turing machines
Example 2: This example illustrates the way a nondeterministic string Turing machine accepts a word of the type-3 language L = a | a(a|b)*a.
A left linear grammar for this language is
| S | 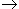 | a | Xa |
| X | 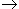 | Xa | Xb |
| X |  | a |
The transition relation of the corresponding string Turing machine contains tupels (1, a, D, Y) for each production of the form Y a and (X, a, D, Y) for each production of the form Y
a and (X, a, D, Y) for each production of the form Y Xa.
Xa.
Language classes recognized by string Turing machines
We have seen that every type-i language is recognizable by a corresponding type of string Turing machine, which we call type-i string Turing machine. We show now that, vice-versa, any language recognized by a type-i string Turing machine is a type-i language.
Theorem: Any language recognized by a type-i string Turing machine is a type-i language (i = 0, 1, 2, 3).
Proof: We show that a type-i string Turing machine for i = 0, 1, 2, 3 can be simulated by a nondeterministic standard Turing machine, linear bounded automaton, pushdown automaton, and finite automaton, respectively. Thus, if a language is recognized, for instance, by a type-2 string Turing machine, it is recognized by a nondeterministic pushdown automaton and therefore is context-free or type-2.
Type 0 and type 1
For string Turing machines of type i = 0, 1 the construction of a corresponding standard Turing machine and linear bounded automaton, respectively, is obvious. As stated before, the actions of a string Turing machine can be simulated by a standard Turing machine. In the same way, the actions of a type-1 string Turing machine can be simulated by a linear bounded automaton.
Type 2
We show in detail the construction of a nondeterministic pushdown automaton from a type-2 string Turing machine.
The input alphabet of the pushdown automaton is the same as that of the string Turing machine and the stack alphabet corresponds to the string alphabet. The pushdown automaton has the same states as the string Turing machine, plus some extra states required by the construction of the transition relation.
The transition relation of a pushdown automaton consists of 5-tuples of the form
(s, a, h, h', s')
where s is the current state, a is the symbol read, h is the topmost stack symbol that is popped from the stack, h' is the symbol pushed to the stack, and s' is the next state. Any of a, h, and h' may be the empty word ε.
We construct the transition relation d' of the pushdown automaton from the transition relation d of the string Turing machine in the following way.
- A tuple of the form (s, a, R, t) of the transition relation d of the string Turing machine means reading some symbol a, performing a move right action, and making a state transition from s to t. The corresponding pushdown automaton simulates this in the following way. It makes sure that symbol a is the topmost stack symbol, reads some input symbol b at the cursor position after the move right action, and pushs this symbol b onto the stack. Moreover, it makes a state transition from s to t. In the transition relation of the pushdown automaton several tuples are needed to accomplish this:
For any tuple
(s, a, R, t) ∈ d
a tuple
(s, ε, a, a, s') ∈ d'
is generated, where s' is a new state of the state set Z' of the pushdown automaton. Hereby the pushdown automaton makes sure that a is the topmost stack symbol, and it performs a state transition to a newly introduced interim state s'.
Moreover, for any tuple
(t, b, b', t') ∈ d
a tuple
(s', b, ε, b, t) ∈ d'
is generated, in order to read input symbol b, push it onto the stack and completing the state transition to state t.
- A tuple of the form (s, a, D, t) means deleting symbol a at the cursor position. The corresponding action of the pushdown automaton is to pop symbol a from the stack.
For any tuple
(s, a, D, t) ∈ d
a tuple
(s, ε, a, ε, t) ∈ d'
in generated.
- A tuple of the form (s, a, a', t) means that symbol a at the cursor position is overwritten by symbol a'. The corresponding action of the pushdown automaton is to pop symbol a from the stack and push symbol a' onto the stack.
For any tuple
(s, a, a', t) ∈ d
a tuple
(s, ε, a, a', t) ∈ d'
is generated.
- Finally, a tuple
(q', $, ε, $, q) ∈ d'
is generated for reading the delimiter symbol $ and pushing it as a bottom symbol onto the stack. State q' is a newly introduced start state of the pushdown automaton, state q is the original start state of the string Turing machine.
If the string Turing machine processes a word w, then the pushdown automaton processes the word $w& in a corresponding way. If the string Turing machine has reduced its string to the empty string and accepts, then the pushdown automaton accepts with empty stack. If, vice versa, the pushdown automaton accepts a word by empty stack, there is a corresponding sequence of transitions by which the string Turing machine reduces this word to the empty string. Thus, if the string Turing machine recognizes some language L, the pushdown automaton recognizes the language $L&.
Any language recognized by a pushdown automaton is context-free. However, if $L& is context-free, then so is L. This can be shown by deleting the symbols $ and & from the context-free grammar for $L&. The resulting grammar is still context-free and generates L.
Therefore, any language recognized by a type-2 string Turing machine is context-free.
Type 3
A type-3 Turing machine essentially acts like a nondeterministic finite automaton that processes the input word from right to left. Thus, if L is the language accepted by the string Turing machine, then &LR$ is the language accepted by the nondeterministic finite automaton, where LR is the mirror image of L. Since &LR$ is regular, so is LR, and so is L, since the mirror image of a regular language is regular.
Conclusions
We have introduced the concept of the string Turing machine as a natural device for recognizing languages.
A string Turing machine can recognize a word by applying reduction steps according to the productions of some grammar. Depending of the type of the grammar, a corresponding type of string Turing machine suffices to recognize the language. We have defined type-i string Turing machines for i = 0, 1, 2, 3 where each type i is a special case of type i-1 using only a proper subset of the cursor actions {L, R, I, D}.
The main result is that the (nondeterministic) type-i string Turing machines correspond exactly to the type-i languages of the Chomsky hierarchy.
References
[HMU 06] J.E. Hopcroft, R. Motwani, J.D. Ullman: Automata Theory, Languages, and Computation. 3rd edition, Addison-Wesley (2006)
[Lan 10] H.W. Lang: A Characterization of the Chomsky Hierarchy by String Turing Machines. In: H.R. Arabnia, G.A. Gravvanis, A.M.G. Solo (Hrsg.): Proceedings of the 2010 International Conference on Foundations of Computer Science, CSREA Press, 109-114 (2010)
[LP 81] H.R. Lewis, C.H. Papadimitriou: Elements of the Theory of Computation. Prentice Hall (1981)
[Sal 73] A.K. Salomaa: Formal Languages. Academic Press (1973)
[Sip 96] M. Sipser: Introduction to the Theory of Computation. PWS Publishing Company (1996)
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 01.02.2010 Updated: 19.02.2023