Parser und Übersetzer

Recursive-Descent-Übersetzung -- systematisch

Wie gelangen wir vom Parser zum Compiler? Wie fügen wir zum Parser geeignete Übersetzungs­aktionen hinzu, um das gewünschte Übersetzungs­ergebnis zu erzielen?

Am Beispiel der Auswertung von Additions-/Subtraktions-Ausdrücken wird im Folgenden eine formale Methode vorgestellt, um systematisch eine Grammatik-Produktion in eine Compiler-Funktion zu überführen.

Auswertung von Ausdrücken

Wir nehmen den Parser zur Auswertung von Additions-/Subtraktions-Ausdrücken als Grundlage, um nunmehr die eingegebenen Ausdrücke nicht nur zu parsen, sondern syntax­gesteuert in ihren Wert zu übersetzen. Zum Beispiel liefert der Ausdruck "9-3-4" als Ergebnis den Wert 2.

Eine Grammatik, die für Recursive-Descent-Übersetzung geeignet ist, lautet folgender­maßen:

expr geht über nachnumber rest
rest geht über nach+ number rest  |  - number rest  |  ε

Leider hat die Beseitigung der Links­rekursionen in der Grammatik auch die Auswertungs­reihenfolge geändert. Der Ableitungs­baum für den Ausdruck "9-3-4" zeigt, dass von rechts nach links zusammen­gefasst wird (Bild 1a). Dennoch ist es möglich, den Ausdruck korrekt auszuwerten, jedoch nur, indem auch Datenfluss von oben nach unten im Baum stattfindet. Bild 1b zeigt den ent­sprechenden Daten­fluss­graphen.

 

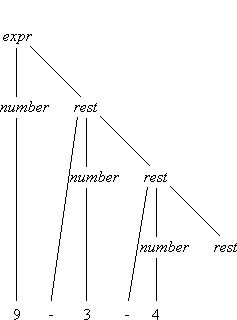
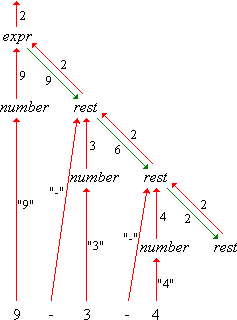
neuer Ableitungsbaum neuer Datenflussgraph 

Bild 1: Ableitungsbaum und Datenflussgraph für den Ausdruck "9-3-4"

 

Übersetzungsaktionen bei Rekursion

Aus der Analyse des Daten­fluss­graphen werden geeignete Übersetzungsaktionen hergeleitet, die zu den Parser-Funktionen hinzugefügt werden. Im Unterschied zu den Parser-Funktionen erzeugen die Compiler-Funktionen nun jeweils einen Wert und bekommen gegebenenfalls einen Wert als Parameter übergeben.1)

Wir beschränken uns im Folgenden auf die Übersetzungs­aktionen in der Compiler-Funktion, die der Produktion rest geht über nach- number rest entspricht.

Betrachten wir beispiels­weise das erste Vorkommen von rest im Daten­fluss­graphen von Bild 1b. Die ent­sprechende Compiler-Funktion rest bekommt die 9 als Parameter übergeben. Sie ruft number auf und subtrahiert den Rückgabewert 3 von 9. Das Ergebnis 6 übergibt sie als Parameter an den rekursiven Aufruf von rest. Den Rückgabewert 2 dieses rekursiven Aufrufs gibt sie ihrerseits als Rückgabewert zurück.

Das folgende Bild 2 zeigt den Ableitungs­baum für eine allgemeine Produktion P0 → P1 P2 P3 und den zugehörigen Daten­fluss­graphen der Übersetzungs­aktionen (die Ver­allgemeinerung für P0 → P1 ... Pn mit beliebigem n ist offen­sichtlich).

 

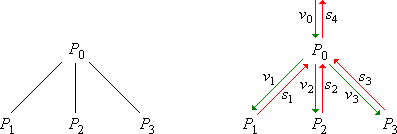
Bild 2: Ableitungsbaum und Datenflussgraph für die allgemeine Produktion P0 → P1 P2 P3 

Bild 2: Ableitungsbaum und Datenflussgraph für die allgemeine Produktion P0 → P1 P2 P3

 

Die ent­sprechenden Übersetzungs­aktionen werden zu der Produktion P0 → P1 P2 P3 nach folgendem Schema hinzugefügt:

Produktion Übersetzungs­aktionen
P0  →   
P1
P2
P3  
 
 s0 = v0
v1 = f1(s0) s1 = P1(v1)
v2 = f2(s0, s1) s2 = P2(v2)
v3 = f3(s0, s1, s2) s3 = P3(v3)
v4 = f4(s0, s1, s2, s3) s4 = v4

Die vi und si sind Programm­variablen. Die Programm­variable v0 ist der Parameter der Funktion P0 und die Programm­variable s4 der Rückgabewert der Funktion P0. Man nennt v0 das vererbte Attribut und s4 das synthetisierte Attribut der Produktion. Die Funktionen fi enthalten die Übersetzungs­aktionen. Die Pi(vi) sind Funktions­aufrufe, die zu den Zeichen Pi gehören. Ist Pi ein Terminal­zeichen, so wird die Funktion match(Pi) aufgerufen.

Konkret angewandt auf die oben angegebene Produktion rest geht über nach- number rest ergibt sich das folgende Schema, indem die ent­sprechenden Zeichen für Pi und die gewünschten Übersetzungs­aktionen für fi eingesetzt werden. Nicht benötigte Variablen sind weggelassen worden.

Produktion Übersetzungs­aktionen
rest →  
 -
 number 
 rest
 
 s0 = v0
 match("-")
 s2 = number()
v3 = s0 – s2   s3 = rest(v3)
v4 = s3 s4 = v4

Welche Übersetzungs­aktionen konkret einzusetzen sind, lässt sich wie oben gesehen am einfachsten durch Analyse des Daten­fluss­graphen eines Beispiel­ausdrucks bestimmen.

So ergeben sich die Berechnungen, die bei Anwendung der Produktion rest geht über nach- number rest auszuführen sind: Die Funktion rest vermindert den Wert, den sie von oben bekommt (v0 = s0 = 9), um den Wert, den sie von number bekommt (s2 = 3). Hieraus ergibt sich die Übersetzungs­aktion v3 = s0 – s2. Das Ergebnis (v3 = 6) übergibt sie als Parameter einem weiteren Aufruf von rest. Den Wert, den sie von diesem Aufruf von rest zurückerhält (s3 = 2), gibt sie ihrerseits zurück (s4 = 2).

Die direkte Implementation der Übersetzungs­aktionen liefert folgendes Programm (Variablen­deklarationen weggelassen):

int rest(int v0){  s0=v0;
                   match("-");
                   s2=number();
v3=s0-s2;          s3=rest(v3);
v4=s3;             return v4;}

 

Die Implementation lässt sich vereinfachen, indem anstelle der Variablen gleich die ent­sprechenden Ausdrücke eingesetzt werden, etwa wie folgt:

int rest(int v0)
{
    match("-");
    return rest(v0-number());
}

Übersetzersetzungsaktionen bei Iteration

Wir hatten gesehen, dass sich Links­rekursion auch durch Iteration beseitigen lässt. Das Ergebnis ist die Grammatik

expr geht über nachnumber rest
rest geht über nach(+ number | - number)*
number geht über nach0  |  1  |  2  |  3  |  4  |  5  |  6  |  7  |  8  |  9

Wir beschränken uns wiederum auf die Produktion rest geht über nach(- number)*.

 

Die allgemeine, formale Vorgehens­weise für das Hinzufügen von Übersetzungs­aktionen bei einer Produktion vom Typ P0 → (P1 P2)* ergibt sich aus folgendem Schema. Zu beachten ist, dass in den sich wieder­holenden Anweisungen innerhalb von ( ... )* zum Schluss wieder die Variable s0 verwendet wird.

Übersetzungs­aktionen
 s0 = v0
( v1 = f1(s0) s1 = P1(v1)
  v2 = f2(s0, s1)   s2 = P2(v2)
  v3 = f3(s0, s1, s2)   s0 = v3 )*

Wir wenden das Schema nun konkret auf die Produktion rest geht über nach(- number)* an, mit rest für P0, - für P1 und number für P2. Nicht benötigte Variablen sind weggelassen worden.

Übersetzungs­aktionen
  s0 = v0
 ( match("-")
   s2 = number()
v3 = s0 – s2     s0 = v3 )*

Die direkte Implementation der Übersetzungs­aktionen liefert folgendes Programm. Die Wiederholung der Anweisungen wird durch eine While-Schleife gesteuert.

int rest(int v0){  s0=v0;
while (comes("-")) {
                   match("-");
                   s2=number();
v3=s0-s2;          s0=v3; }
return s0; }

 

Die Implementation lässt sich vereinfachen, indem anstelle der Variablen gleich die ent­sprechenden Ausdrücke eingesetzt werden:

int rest(int v0)
{
    while (comes("-"))
    {
        match("-");
        v0=v0-number();
    }
    return v0;
}

 

Zusammenfassung

Aus der Untersuchung des Daten­fluss­graphen, der einem konkreten Ableitungs­baum entspricht, lassen sich geeignete Übersetzungs­aktionen ableiten. Indem diese jeweils in das formale Schema eingesetzt werden, ergibt sich die ent­sprechende Compiler-Funktion.

Wir haben ein solches formales Schema sowohl für die rekursive Form einer Produktion als auch für die iterative Form angegeben. Das formale Schema enthält eine Vielzahl von Variablen für die jeweiligen Zwischen­ergebnisse. In der konkreten Implementierung können meist etliche dieser Variablen eingespart werden.

Aufgaben

Aufgabe 1:  Wenden Sie das formale Vorgehen bei der Konstruktion eines Übersetzers für mehrstellige ganze Zahlen an. Der Übersetzer soll eine als String gegebene Zahl in ihren Zahlenwert übersetzen, z.B. den String "00365" in den Wert 365. Verwenden Sie dabei folgende Grammatik:

number geht über nachdigit moredigits
moredigits geht über nachdigit*
digit geht über nach0  |  1  |  2  |  3  |  4  |  5  |  6  |  7  |  8  |  9

1)  Der Begriff Wert ist nicht wie in diesem Beispiel auf einen Zahlenwert beschränkt, sondern der Wert kann auch ein String oder eine Referenz auf ein beliebiges Objekt sein.

 

Weiter mit:   [up]

 

H.W. Lang   mail@hwlang.de   Impressum   Datenschutz
Created: 02.12.2011   Updated: 17.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden