Parser und Übersetzer
Recursive-Descent-Methode
Die Methode der Übersetzung durch rekursiven Abstieg (engl.: recursive descent) wird im Folgenden anhand von Beispielen dargestellt. Das erste Beispiel ist bewusst sehr einfach gewählt, um das Prinzip der Recursive-Descent-Methode darzustellen.
In diesem Beispiel wird ein Parser für Zeichenfolgen, die einstellige ganze Zahlen mit oder ohne Vorzeichen darstellen, konstruiert. Ein Parser ist ein Programm, das ein Eingabewort in seine syntaktischen Bestandteile zerlegt und erkennt, ob es den vorgegebenen Syntaxregeln entspricht oder nicht.
Syntax
Die Syntaxregeln werden formal durch eine kontextfreie Grammatik angegeben. In unserem Beispiel bestehen die Zahlen zunächst nur aus einer Ziffer. Das Vorzeichen ist ein Plus- oder ein Minuszeichen oder es fehlt. Wir benutzen folgende Grammatik G = (V, T, P, S); es sind
| V = | {number, sign, digit} die Menge der Variablen, | ||||||||||
| T = | { 0, ..., 9, +, - } die Menge der Terminalzeichen, | ||||||||||
| P : |
| ||||||||||
| die Produktionen und | |||||||||||
| S = | number das Startsymbol. |
Syntaktisch korrekte Zeichenfolgen entsprechend dieser Grammatik sind also beispielsweise 3, -5, +0 oder +6. Bild 1 zeigt den Ableitungsbaum für -5.
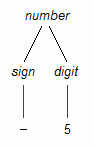
Bild 1: Ableitungsbaum für -5
Recursive-Descent-Methode
Bei der Recursive-Descent-Methode wird für jede Variable, die auf der linken Seite einer Produktion vorkommt, eine Funktion geschrieben. In der Funktion wird die rechte Seite der jeweiligen Produktion behandelt. Für jede dort vorkommende Variable wird ein entsprechender Funktionsaufruf durchgeführt, für jedes Terminalzeichen wird das entsprechende Zeichen vom Eingabewort abgearbeitet.
Durch Aufruf der Funktion, die dem Startsymbol der Grammatik entspricht, steigt das Verfahren rekursiv im Ableitungsbaum hinab bis zum Eingabewort, das sich an den Blättern des Ableitungsbaumes befindet – daher die Bezeichnung recursive descent.
Das Startsymbol der oben angegebenen Grammatik ist number. Die Funktion number besteht, entsprechend der Produktion für number, aus einem Funktionsaufruf für sign gefolgt von einem Funktionsaufruf für digit.
sign()
digit()
Hat eine Produktion auf der rechten Seite mehrere Alternativen, so wird in der Funktion eine entsprechende Fallunterscheidung durchgeführt. Grundlage der Entscheidung, welche Alternative angewendet wird, ist das nächste abzuarbeitende Zeichen des Eingabewortes (der Lookahead). Die Grammatik muss so gestaltet sein, dass aufgrund des Lookaheads immer eine Entscheidung möglich ist.
Die Funktion für die Variable sign unterscheidet die beiden Alternativen der Produktion in entsprechender Weise: Wenn das nächste Zeichen des Eingabewortes ein Pluszeichen ist, wird die erste Alternative angewendet, wenn es ein Minuszeichen ist, wird die zweite Alternative angewendet, anderenfalls die dritte.
Die Funktion comes prüft das nächste Zeichen des Eingabewortes; die Funktion consume arbeitet das Zeichen ab. Die genaue Implementierung dieser Funktionen ist im Basismodul Parser angegeben.
if comes("+"):
consume()
elif comes("-"):
consume()
else:
pass # Epsilon-Produktion: tue nichts
Der Else-Teil für die Anwendung der Epsilon-Produktion ist hier nur der Deutlichkeit halber angegeben; da er nichts bewirkt, kann er auch entfallen.
Die Funktion für die Variable digit behandelt alle Alternativen in gleicher Weise und ist daher recht einfach. Mit comesDigit wird geprüft, ob das nächste Zeichen des Eingabewortes eines der Zeichen "0", ..., "9" ist, mit consume wird es dann abgearbeitet. Wenn keine Ziffer gefunden wird, löst die Funktion einen Fehler aus. Der Fehler wird in einer übergeordneten Funktion abgefangen und ausgewertet.
if comesDigit():
consume()
else:
raise Exception("Ziffer erwartet")
Modul SimpleNumberParser
Die angegebenen drei Funktionen für die Variablen der Grammatik sind Bestandteil des Moduls SimpleNumberParser. Es enthält außerdem noch die Funktion comesDigit, die prüft, ob der noch nicht abgearbeitete Teil des Eingabewortes mit einer Ziffer beginnt. Das Modul importiert die grundlegenden Funktionen comes, comesAnyOf und consume aus dem Basismodul Parser.
def number():
sign()
digit()
def sign():
if comes("+"):
consume()
elif comes("-"):
consume()
else:
pass # Epsilon-Produktion: tue nichts
def digit():
if comesDigit():
consume()
else:
raise Exception("Ziffer erwartet")
def comesDigit():
return comesAnyOf("0123456789")
Im Hauptprogramm wird der SimpleNumberParser dann folgendermaßen getestet, hierbei wird der Funktion parse das Eingabewort und der Name der Funktion, die dem Startsymbol der Grammatik entspricht, übergeben.
parse("-5", number)
showErrorPosition()
Im Fehlerfall, etwa bei Eingabe des Wortes - -5, wird die Fehlerposition mit showErrorPosition ausgegeben:
-^
Ziffer erwartet
Zusammenfassung
Eine kontextfreie Grammatik besteht aus Regeln zur Erzeugung von Wörtern einer Sprache. Um ein bestimmtes Wort zu erzeugen, wird ausgehend vom Startsymbol der Grammatik eine bestimmte Folge von Ableitungsschritten, also Anwendungen von Produktionen, ausgeführt. Einer solchen Ableitungsfolge entspricht ein Ableitungsbaum für das Wort (vgl. Bild 1).
Ein Recursive-Descent-Parser erzeugt implizit diesen Ableitungsbaum und durchläuft ihn dabei. Damit dies in deterministischer Weise funktioniert, muss die Grammatik bestimmte Eigenschaften haben; diese werden wir im Einzelnen noch angeben.
Die Systematik der Umformung von Produktionen der Grammatik in entsprechende Funktionen des Parsers ist im Abschnitt über die Erweiterte Backus-Naur-Form für Produktionen angegeben.
In den folgenden Teilen finden sich weitere Beispiele für die Erzeugung von Recursive-Descent-Parsern.
Weiter mit: [Recursive-Descent-Parser für mehrstellige Zahlen] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 16.08.2012 Updated: 17.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
