Formale Verifikation - Aufgaben

Aufgabe:  (Ganzzahlige Wurzel)

Gegeben sei folgendes Programm X mit ganzzahligen Variablen a, x, y und z:

x=0;
y=1;
z=1;
while (y<=a)
{
    x=x+1;
    z=z+2;
    y=y+z;
}

Das Programm soll die ganzzahlige Quadratwurzel x von a berechnen, d.h. es soll gelten x  a  x+1.

Beweisen Sie, dass die Nachbedingung

R:   x²a 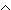   a < (x+1)²

gilt, falls die Schleife terminiert.

Benutzen Sie als Schleifeninvariante

P:   x²a 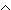   y = x²+z  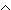  z = 2x+1