Formale Verifikation - AufgabenSumme | 
|
Aufgabe: (Summe der Zahlen von 1 bis n)
Gegeben sei folgendes Programm X:
s=0;
i=0;
while (i<=n)
{
s=s+i;
i=i+1;
}
|
Das Programm X soll die Summe der Zahlen von 0 bis n berechnen.
Beweisen Sie {Q} X {R} mit der Vorbedingung
Q: n
0
und der Nachbedingung
| R: s = |
|
Verwenden Sie als Schleifeninvariante
P: 2s = (i-1)·i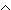 
i-1
n.
Anmerkung (14.09.2010): Man kann sogar die Vorbedingung Q': n-1 beweisen. Durch Verschärfung erhält man die geforderte Vorbedingung Q: n0.
Da aber tatsächlich auch die Vorbedingung Q': n-1 gilt, kann das Programm die Summe der Zahlen von 1 bis -1 berechnen. Die Folge der Zahlen, die bei 1 beginnt und bei -1 endet, ist aber leer. Die Summe der Zahlen, die sich in der leeren Menge befinden, ist 0. Die Formel R stimmt also (mehr oder weniger zufällig) auch für n = -1 und das Programm rechnet korrekt.
Schöner wäre es, wenn Q: n0 als schwächste Vorbedingung herauskommen würde. Dies wird erreicht, indem als zweite Programmzeile i=1; gesetzt wird. Damit ergibt sich ein in sich schlüssigeres Programm.
Weiter mit:
 |
 H.W. Lang Fachhochschule Flensburg lang@fh-flensburg.de Impressum © |
 |