Formale Verifikation - Aufgaben

Aufgabe:  (Summe der Quadrat­zahlen von 1 bis n)

Gegeben sei folgendes Programm X:

s=0;
i=0;
while (i<n)
{
    i=i+1;
    q=i*i;    
    s=s+q;
}

Das Programm X soll die Summe der Quadrate der Zahlen von 1 bis n berechnen.

Beweisen Sie {Q} X {R} mit der Vorbedingung

Q:   n0

und der Nach­bedingung

R:   s  =  (2n³ + 3n² + n) / 6

Verwenden Sie als Schleifen­invariante

P:   6s  =  2i³ + 3i² + i 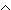   in.