Formale Verifikation - Aufgaben

Aufgabe:  (Euklidischer Algorithmus – partielle und totale Korrektheit)

Gegeben sei folgendes Programm X mit int-Variablen a, b, x, y und r:

x=a;
y=b;
while (y!=0)
{
    r=x%y;
    x=y;
    y=r;
}

Das Programm soll den größten gemeinsamen Teiler von a und b berechnen.

Beweisen Sie die partielle Korrektheit von X bezüglich der Vorbedingung Q:  true und der Nach­bedingung

R:   ggt(a, b) = ggt(x, y) 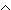   y = 0.

Aus der Nach­bedingung folgt, dass x der größte gemeinsame Teiler von a und b ist, denn es gilt

ggt(a, b) = ggt(x, y) 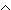   y = 0 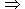     ggt(a, b) = ggt(x, 0) = x.

Benutzen Sie beim Beweis des Schleifen­körpers, dass

ggt(x, y)  =  ggt(y, x mod y)

gilt, falls y ≠ 0 ist.