Formale Verifikation - Aufgaben

Aufgabe:  (Ganzzahlige Division – partielle und totale Korrekheit)

Gegeben sei folgendes Programm X mit ganzzahligen Variablen a, b, q und r:

q=0;
r=a;
while (r>=b)
{
    q=q+1;
    r=r-b;
}

Das Programm soll den Rest r bei ganzzahliger Division von a durch b berechnen.

Beweisen Sie, dass die Nach­bedingung

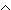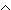R:   a = q·b + r    r0    r < b

gilt, falls die Schleife terminiert (partielle Korrektheit).

Wie lautet die Schleifen­invariante P? Welches ist die schwächste Vorbedingung Q des Programms?

Für den Beweis der totalen Korrektheit muss die Schleifen­invariante P verschärft werden, damit es einen ganzzahliger Ausdruck E gibt, der im Schleifen­körper vermindert wird und für den E > 0 aus P 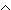 B abgeleitet werden kann.