Flächeninhalt eines Dreiecks

Normaler­weise berechnest du den Flächen­inhalt eines Dreiecks nach der Formel Grundlinie mal Höhe / 2. Oft kennst du allerdings diese Größen nicht; beispiels­weise sind nur die Eckpunkte des Dreiecks gegeben oder nur die Seitenlängen. Dann wendest du die folgenden Formeln an.

Eckpunkte gegeben

Gegeben sind die drei Eckpunkte P1, P2, P3 des Dreiecks im positiven Umlaufsinn. Gesucht ist der Flächen­inhalt des Dreiecks. Im folgenden Bild siehst du, dass sich die Dreiecks­fläche als Summe von drei Trapez­flächen ergibt.

 

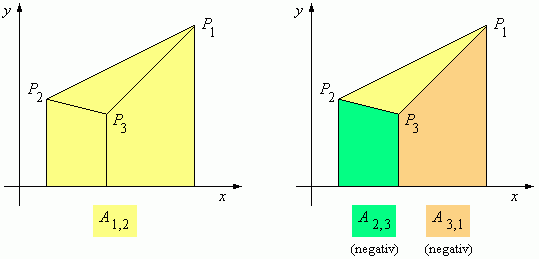
Bild 1: Dreiecksfläche als Summe von drei Trapezflächen  

Bild 1: Dreiecksfläche als Summe von drei Trapezflächen

 

Der Flächen­inhalt des gelben Trapezes ist

A1,2   =   (x1 – x2)  ·  
(y1 + y2)
2

Auf dieselbe Art und Weise rechnest du den Flächen­inhalt des grünen Trapezes aus:

A2,3   =   (x2 – x3)  ·  
(y2 + y3)
2

Der Flächen­inhalt ist negativ, weil x2 < x3 ist.

Der Flächen­inhalt des orangenen Trapezes ist ebenfalls negativ, weil x3 < x1 ist:

A3,1   =   (x3 – x1)  ·  
(y3 + y1)
2

 

Der Flächen­inhalt A des Dreiecks ergibt sich also als Summe aller drei Trapeze:

A   =   A1,2 + A2,3 + A3,1   =   
(x1 – x2)·(y1 + y2)  +  (x2 – x3)·(y2 + y3)  +  (x3 – x1)·(y3 + y1)
2

Du bildest also die Differenzen der x-Werte aufeinander­folgender Punkte und multi­pliziert diese mit den Summen der zugehörigen y-Werte, das ganze einmal um das Dreieck herum. Wichtig ist dabei, dass die Eckpunkte im positiven Umlaufsinn bezeichnet sind.

Die Formel ist auch dann gültig, wenn die Eckpunkte des Dreiecks nicht, wie hier, alle oberhalb der x-Achse liegen. Außerdem lässt sich die Formel auch für beliebige Vielecke ver­allgemeinern.

 

Aufgabe 1:  Gegeben sind folgende Eckpunkte eines Dreiecks:

P1 = (-3, -1),   P2 = (4, -2),   P3 = (2, 6)

Berechne den Flächen­inhalt des Dreiecks.

Lösung:     

 

Seitenlängen gegeben

Gegeben sind die drei Seitenlängen a, b, c des Dreiecks. Gesucht ist der Flächen­inhalt des Dreiecks. Dann kannst du den Flächen­inhalt A nach der Formel von Heronzur Personberechnen:

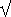A   =   Wurzels·(s – a)·(s – b)·(s – c)

wobei

s   =   
a + b + c
2

der halbe Umfang des Dreiecks ist.

 

Aufgabe 2:  Gegeben sind folgende Seitenlängen eines Dreiecks:

a = 3,   b = 4,   c = 5

Berechne den Flächen­inhalt des Dreiecks.

Lösung:     

 

[up]

 

H.W. Lang   mail@hwlang.de   Impressum   Datenschutz
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden