Kryptografische Protokolle
Äquivalenz zwischen Faktorisierung von n und Berechnung von φ(n)
Die Sicherheit der RSA-Verschlüsselung beruht darauf, dass nur n bekannt ist, nicht aber φ(n). Ein Angreifer, dem es gelingt, φ(n) ausfindig zu machen, kann aus dem öffentlichen Schlüssel e den privaten Schlüssel d als das multiplikativ inverse Element modulo φ(n) berechnen.
Beim RSA-Verfahren ist die Zahl n das Produkt aus zwei verschiedenen Primzahlen p und q. Öffentlich bekannt ist aber nur die Zahl n, jedoch nicht die beiden Faktoren p und q, aus denen sich n zusammensetzt. Bei kleinen Zahlen, etwa n = 77, lassen sich die Faktoren leicht ermitteln, bei sehr großen Zahlen, etwa Zahlen der Länge 1024 Bit, jedoch nicht. Nach heutigem Stand ist die Faktorisierung von großen Zahlen undurchführbar, weil zu rechenaufwendig.
Jeder, der p und q ausfindig machen kann, ist in der Lage, φ(n) zu berechnen, mittels der Formel
φ(n) = (p-1)·(q-1)
Die Berechnung von φ(n) ist also höchstens so schwer wie die Faktorisierung von n, also die Zerlegung von n in die Faktoren p und q.
Aber vielleicht lässt sich ja φ(n) auf andere Art und Weise sehr viel leichter bestimmen, ohne die Zahl n vorher zu faktorisieren? Die Antwort ist nein. Im Folgenden wird gezeigt, dass die Berechnung von φ(n) mindestens so schwer ist wie die Faktorisierung von n.
Denn jeder, der φ(n) bestimmen kann, ist auch in der Lage, p und q zu berechnen. Dies wird im Folgenden gezeigt.
Berechnung von p und q aus n und φ(n)
Es seien n und φ(n) gegeben; wir berechnen daraus p und q.
Als erstes berechnen wir den Wert von p + q aus n und φ(n):
| φ(n) | = | (p-1)·(q-1) | ||
| = | pq – p – q + 1 | |||
| = | n – (p+q) + 1 |
⇒ p + q = n – φ(n) + 1
Wir erzeugen nun eine quadratische Gleichung, deren Lösungen p und q sind:
Diese quadratische Gleichung lässt sich mit der Formel von Vieta lösen (die auch als p-q-Formel bezeichnet wird, wobei jedoch p und q dort eine andere Bedeutung haben als die hier vorkommenden Faktoren p und q). Die beiden Lösungen der quadratischen Gleichung sind die gesuchten Faktoren p und q.
Insgesamt ist damit gezeigt, dass die Berechnung von φ(n) genauso schwer ist wie die Faktorisierung von n.
Zahlenbeispiel
Gegeben seien n = 77 und φ(n) = 60; gesucht ist die Faktorisierung n = p·q.
Es ist zunächst
n – φ(n) + 1 = 77 – 60 + 1 = 18
Die quadratische Gleichung lautet somit
x2 – 18·x + 77
Die Formel von Vieta liefert die Lösungen
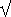81 – 77ausrechnen = 9 ± 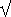4ausrechnen = 9 ± 2
Die beiden Lösungen lauten also x1 = 9 + 2 = 11 und x2 = 9 – 2 = 7.
Wir haben also aus n = 77 und φ(n) = 60 die Faktorisierung 77 = 11 · 7 berechnet.
Übung
Aufgabe 1:
Gegeben sind n = 2911 und φ(n) = 2800. Zerlegen Sie n in die Primfaktoren p und q.
Hinweis: Wenn Sie es sich einfach machen wollen, berechnen Sie n – φ(n) + 1 = 2911 – 2800 + 1 = 112 und tragen dann -112 und 2911 in das Formular zur Lösung einer quadratischen Gleichung ein. Die beiden Lösungen sind die gesuchten Faktoren von n.
Aufgabe 2:
Gegeben sind n = 293141 und φ(n) = 292032. Zerlegen Sie n in die Primfaktoren p und q.
Literatur
[RSA 78] R.L. Rivest, A. Shamir, L.M. Adleman: A Method for Obtaining Digital Signatures and Public-Key Cryptosystems. Communications of the ACM, 21, 2, 120-126 (1978)
[KK 10] C. Karpfinger, H. Kiechle: Kryptologie. Vieweg+Teubner (2010)
[Lan 18] H.W. Lang: Kryptografie für Dummies. Wiley (2018)
Zurück zu: [RSA-Verschlüsselung] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 07.12.2017 Updated: 17.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden