Berechnungsverfahren

Steinscher Algorithmus zur Berechnung des ggt

In der Kryptografie ist die Berechnung des größten gemeinsamen Teilers (ggt) eine häufige Aufgabe. Der euklidische Algorithmus löst diese Aufgabe effizient, allerdings erfordert er die Berechnung der mod-Funktion, also im Prinzip eine Division mit Rest. Mit dem steinschen Algorithmus [Stein 67] lässt sich der größte gemeinsame Teiler ohne Divisionen berechnen. Der steinsche Algorithmus benutzt lediglich Division durch 2; diese lässt sich durch eine Schiebeoperation effizient realisieren.

Der steinsche Algorithmus basiert auf folgenden Rekursionen:

ggt(a, b) = 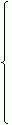geschweifte Klammer

a falls b = 0

ggt(b, a) falls a < b

2·ggt(a/2, b/2) falls a und b gerade

ggt(a/2, b) falls a gerade und b ungerade

ggt(a, b/2) falls a ungerade und b gerade

ggt(a-b, b) falls a und b ungerade

Eine entsprechende Implementierung in der Programmiersprache Haskell ist die folgende:

-- steinscher Algorithmus
ggt :: Integer->Integer->Integer
ggt a b | b==0             = a
        | a < b            = ggt b a
        | even a && even b = 2 * ggt a' b'
        | even a           = ggt a' b
        | even b           = ggt a  b'
        | otherwise        = ggt (a-b) b
        where a' = a `div` 2
              b' = b `div` 2

In der Programmiersprache Python ergibt sich folgende Implementierung:

# steinscher Algorithmus zur Berechnung des ggt, rekursiv
def ggt(a, b):
    if b==0:
        return a
    if a<b:
        return ggt(b, a)
    if a%2==0 and b%2==0:
        return 2 * ggt(a//2, b//2)
    if a%2==0:
        return ggt(a//2, b)
    if b%2==0:
        return ggt(a, b//2)
    else:
        return ggt(a-b, b)

In einer iterativen Implementierung ergibt sich folgendes Programm. Divisionen durch 2 und Multiplikationen mit 2 sind durch Schiebeoperationen realisiert, Modulo-2-Operationen durch bitweises Und mit 1.

# steinscher Algorithmus zur Berechnung des ggt, iterativ
def ggt_iter(a, b):
    f=0
    while b!=0:
        if a<b:
            a, b = b, a
        else:
            if a&1==0:     # a gerade
                a>>=1
                if b&1==0:
                    b>>=1
                    f+=1
            else:          # a ungerade
                if b&1==0:
                    b>>=1
                else:
                    a-=b
    return a<<f

Wir analysieren die rekursive Implementation. Es gibt zwei Arten von rekursiven Aufrufen: Bei der einen Art wird eine Halbierung mindestens eines der Argumente durchgeführt. Bei der anderen Art wird eine Vertauschung der Argumente oder eine Subtraktion der Argumente durchgeführt.

Niemals aber werden mehrere Vertauschungen oder mehrere Subtraktionen hintereinander durchgeführt. Nach maximal einer Subtraktion und einer Vertauschung wird eine Halbierung mindestens eines Arguments durchgeführt.

Es sind also höchstens 3 · (log(a) + log(b)) rekursive Aufrufe erforderlich.

[Stein 67] J. Stein: Computational problems associated with Racah algebra. Journal of Computational Physics, Vol. 1, No. 3, 397–405 (1967)

Weiter mit: [up]

H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 12.10.2014 Updated: 17.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden

Berechnungsverfahren

Steinscher Algorithmus zur Berechnung des ggt

Implementierung

Analyse

Literatur