Datenanalyse

Lineare Regression

Gegeben ist eine Menge von Punkten in der x-y-Ebene, beispiels­weise eine Menge von Messwerten, bei denen ein linearer Zusammenhang vermutet wird, etwa Gewicht (y-Wert) in Abhängigkeit von der Größe (x-Wert).

Gesucht ist eine Gerade, genannt Regressions­gerade, die diesen linearen Zusammenhang der Messwerte bestmöglich wiedergibt.

Bild 1 zeigt eine solche Regressions­gerade, die durch die entsprechenden Punkte führt.

 

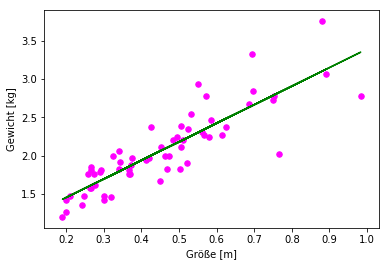
Bild 1: Messwerte und Regressionsgerade 

Bild 1: Messwerte und Regressionsgerade

 

Berechnung

Die Formel für die Berechnung der Steigung m der Regressions­geraden lautet

m   =   
n · Summe xi·yi  –  ( Summe xi) · ( Summe yi)
n · Summe xi2  –  ( Summe xi)2

 

Summiert wird jeweils über i = 0, ..., n-1, wobei n die Anzahl der Werte ist.

Indem statt mit den Summen der xi bzw. yi mit den entsprechenden Mittelwerten x bzw. y gerechnet wird, ergibt sich die Formel

m   =   
 Summe xi·yi  –  n · x · y
 Summe xi2  –  n · x 2(vertikaler Abstand)

 

Implementierung

Es folgt eine Implementierung in der Programmier­sprache Python. Vor Aufruf der folgenden Funktionen müssen die Programm­bibliotheken numpy und matplotlib importiert werden (siehe unten vor dem Aufruf des Test­programms).

 

# Parameter x, y sind numpy-Arrays von Koordinaten
# Rückgabewerte sind Steigung m und y-Achsenabschnitt b
# der berechneten Regressionsgeraden
def computeRegressionLine(x, y): 
    # Anzahl der Punkte
    n = x.size 

    # Mittelwerte der x- und der y-Koordinaten
    mx, my = np.mean(x), np.mean(y) 

    # Regressionsgerade berechnen
    s_xy = np.sum(x*y) - n*my*mx 
    s_xx = np.sum(x*x) - n*mx*mx
    
    # Geradengleichung y = mx + b
    m = s_xy / s_xx 
    b = my - m*mx 

    return m, b

 

Grafische Darstellung

 

# zeichnet die Punkte (x, y) sowie die
# Gerade mx+b
def plotRegressionLine(x, y, m, b, axx="x", ayy="y"): 
    # Punkte zeichnen 
    plt.scatter(x, y, color="magenta", marker="o", s=30) 

    # y-Werte der Regressionsgeraden
    y_g = m*x + b

    # Regressionsgerade zeichnen
    plt.plot(x, y_g, color="green") 

    # Achsenbeschriftungen
    plt.xlabel(axx) 
    plt.ylabel(ayy) 

    plt.show() 

 

Testprogramm

 

import numpy as np 
import matplotlib.pyplot as plt

# Test Regressionsgerade
def main(): 
    # Punkte
    x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) 
    y = np.array([1, 3, 2, 5, 7, 8, 8, 9, 10, 12]) 

    # Regressionsgerade berechnen
    m, b = computeRegressionLine(x, y)
    print("Regressionsgerade y = mx + b")
    print("m =",m)
    print("b =",b)

    # Regressionsgerade zeichnen 
    plotRegressionLine(x, y, m, b) 

main()

Bibliotheksfunktion

Unter Benutzung des Moduls stats aus der Bibliothek scipy lässt sich die Regressions­gerade auch folgender­maßen berechnen:

from scipy import stats
m, b, r_val, p_val, std_err=stats.linregress(x, y)

 

Weiter mit:   [up]

 

H.W. Lang   mail@hwlang.de   Impressum   Datenschutz
Created: 09.12.2018   Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden