Sorting on two dimensional processor arrays
2d odd-even transposition sort
The simplest algorithm for sorting two-dimensional arrays is 2d odd-even transposition sort. Unfortunately, it has a time complexity of Θ(n2), which is slow.
Idea
The idea of odd-even transposition sort is generalized to two-dimensional arrays in a straightforward way. Figure 1 shows the two steps of one-dimensional odd-even transposition sort that are repeated in alternating order.
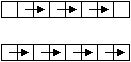
Figure 1: One-dimensional odd-even transposition sort
In two-dimensional odd-even transposition sort, the elements are not just compared with their right and left neighbours, but also with their upper and lower neighbours. The sorting direction in the array is snake-like. Figure 2 shows the four steps of two-dimensional odd-even transposition sort that are repeated in round-robin order.
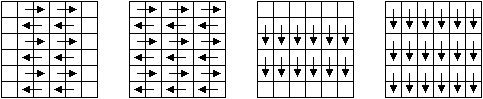
Figure 2: Two-dimensional odd-even transposition sort
Algorithm
In the following algorithm, with oets step a step of odd-even transposition sort is denoted.
Algorithhm 2d odd-even transposition sort
Input:
unsorted n × n-array
Output:
the array sorted in snake-like order
Method:
- while the array is not sorted do
- apply an odd oets step to the rows
- apply an even oets step to the rows
- apply an odd oets step to the columns
- apply an even oets step to the columns
The sorting direction of the rows must be alternating, i.e. even rows from left to right and odd rows from right to left.
A simulation shows the crucial point of the algorithm: It sorts a random input of 0's and 1's remarkably fast. However, in the worst case, it is slow. Actually, the time complexity in the worst case is θ(n2), due to a behavior known as sand dune effect. The sand dune effect occurs also with random inputs of values drawn from a larger set than just the two values 0 and 1.
Next: [Shearsort] or [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 29.11.2004 Updated: 07.02.2023