Sortiernetze
Minimale Sortiernetze mit mehr als 8 Eingängen
| 
|
Wir hatten zunächst minimale Sortiernetze mit bis zu n = 8 Eingängen betrachtet.
Die folgende Tabelle zeigt die Anzahl V(n) der Vergleicher, die für Sortiernetze mit n > 8 Eingängen höchstens erforderlich sind [Knu 73]. Der Wert V(n) für n = 13 hat sich gegenüber 46 in [Knu 73] inzwischen auf 45 verbessert.
Die unteren Schranken U(n) haben sich gegenüber den bisher bekannten Angaben in [BB 11] erst kürzlich verbessert, dadurch dass U(9) = 25 bewiesen wurde [CCFS 14]. Wegen U(n+1)  U(n) +
U(n) + 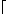 log2(n)
log2(n)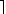 haben sich die unteren Schranken ab n = 10 entsprechend verschoben. Damit sind die Sortiernetze N9 und N10 optimal.
haben sich die unteren Schranken ab n = 10 entsprechend verschoben. Damit sind die Sortiernetze N9 und N10 optimal.
| n | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|
| V(n) | 25 | 29 | 35 | 39 | 45 | 51 | 56 | 60 |
|---|
| U(n) | 25 | 29 | 33 | 37 | 41 | 45 | 49 | 53 |
|---|
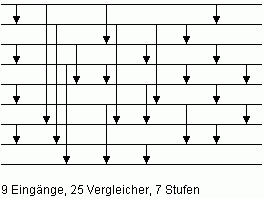
Die folgenden Abbildungen zeigen die entsprechenden (bisher bekannten) minimalen Sortiernetze mit n > 8 Eingängen:
|
|
| Bild 1: Minimales Sortiernetz N9 für n = 9 |
|
|
|
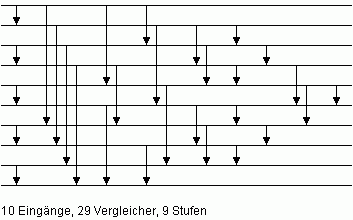
| Bild 2: Minimales Sortiernetz N10 für n = 10 |
|
|
|
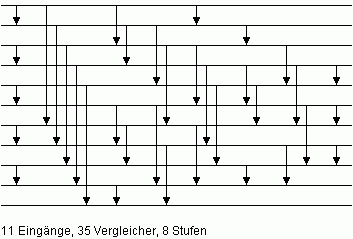
| Bild 3: Minimales Sortiernetz N11 für n = 11 |
|
|
|
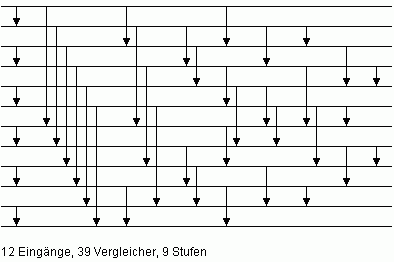
| Bild 4: Minimales Sortiernetz N12 für n = 12 |
|
|
|
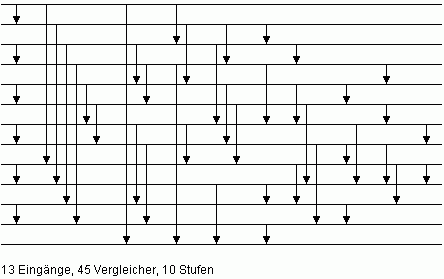
| Bild 5: Minimales Sortiernetz N13 für n = 13 |
|
|
|
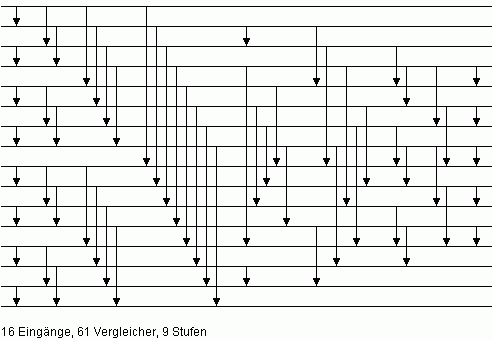
| Bild 6: Minimales Sortiernetz N16 für n = 16 |
|
Die Sortiernetze N14 und N15 entstehen durch Einschränkung von N16 auf die oberen 14 bzw. 15 Eingänge.
Es gibt eine ganze Reihe anderer minimaler Sortiernetze für die jeweilige Anzahl n von Eingängen. Teilweise ergeben sich diese jedoch lediglich durch Umordnen der Eingänge aus den oben dargestellten Sortiernetzen.
Die folgende Tabelle gibt für n > 8 einen Überblick über die Anzahl S(n) der Vergleicherstufen, die in einem Sortiernetz mit n Eingängen höchstens erforderlich sind [Knu 73]. Gleichzeitig stellen die Werte von S(n) auch untere Schranken für die Anzahl der Vergleicherstufen dar; diese Tatsache ist erst kürzlich bewiesen worden [BZ 14]. Hinsichtlich der Anzahl der Vergleicherstufen sind die unten dargestellten Sortiernetze somit optimal.
| n | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|
| S(n) | 7 | 7 | 8 | 8 | 9 | 9 | 9 | 9 |
|---|
In den folgenden Abbildungen sind entsprechende Sortiernetze mit (bisher bekannter) minimaler Anzahl von Vergleicherstufen dargestellt, soweit sie weniger Vergleicherstufen haben als die oben dargestellten Sortiernetze N9, ..., N16.
|
|
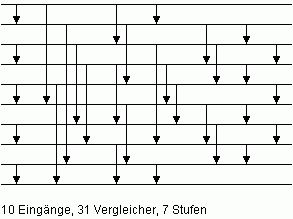
| Bild 7: Sortiernetz M10 mit minimaler Anzahl von Vergleicherstufen für n = 10 |
|
|
|
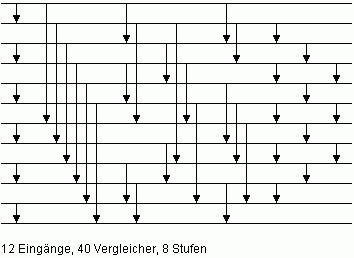
| Bild 8: Sortiernetz M12 mit minimaler Anzahl von Vergleicherstufen für n = 12 |
|
|
|
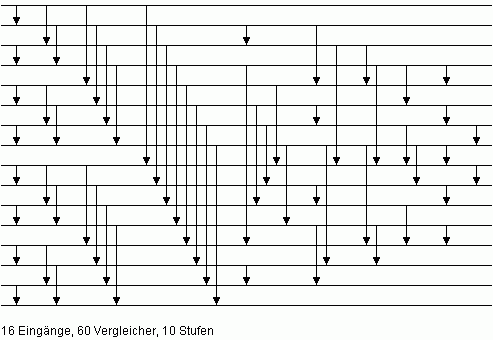
| Bild 9: Sortiernetz M16 mit minimaler Anzahl von Vergleicherstufen für n = 16 |
|
Wiederum entstehen die Sortiernetze M13, M14 und M15 durch Einschränkung von M16 auf die oberen 13, 14 bzw. 15 Eingänge.
Die folgenden Tabellen geben Auskunft über die bisher bekannten oberen Schranken V(n) und unteren Schanken U(n) für die Anzahl der Vergleicher eines Sortiernetzes mit n Eingängen, ferner über die bisher bekannten oberen Schranken S(n) und unteren Schranken R(n) für die Anzahl der Vergleicherstufen [BB 11], [BZ 14].
| n | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
|---|
| V(n) | 73 | 80 | 88 | 93 | 103 | 110 | 118 | 123 | 133 | 140 | 150 | 156 | 165 | 172 | 180 | 185 |
|---|
| U(n) | 58 | 63 | 68 | 73 | 78 | 83 | 88 | 93 | 98 | 103 | 108 | 113 | 118 | 123 | 128 | 133 |
|---|
Anzahl der Vergleicher: obere und untere Schranken
| n | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
|---|
| S(n) | 11 | 11 | 12 | 12 | 12 | 12 | 13 | 13 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 |
|---|
| R(n) | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
|---|
Anzahl der Vergleicherstufen: obere und untere Schranken
| | |
| [BB 11] | S.W. Al-Haj Baddar, K.E. Batcher: Designing Sorting Networks. Springer (2011) |
| [BZ 14] | D. Bundala, J. Závodný: Optimal Sorting Networks. In: A.H. Dediu et al. (Hrsg.): Lecture Notes in Computer Science 8370, 236-247 (2014) |
| [CCFS 14] | M. Codish, L. Cruz-Filipe, M. Frank, P. Schneider-Kamp: Twenty-Five Comparators is Optimal when Sorting Nine Inputs (and Twenty-Nine for Ten). arXiv:1405.5754 (2014) |
| [Knu 73] | D.E. Knuth: The Art of Computer Programming, Vol. 3 - Sorting and Searching. Addison-Wesley (1973) |
Weiter mit:
 |
 U(n) +
U(n) + 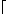 log2(n)
log2(n) haben sich die unteren Schranken ab n = 10 entsprechend verschoben. Damit sind die Sortiernetze N9 und N10 optimal.
haben sich die unteren Schranken ab n = 10 entsprechend verschoben. Damit sind die Sortiernetze N9 und N10 optimal.