AlgorithmenObere und untere Schranken | |
Obere Schranken
Im Sommerschlussverkauf wird vielfach geworben mit Angaben wie
Preise bis zu 70% reduziert
Dies bedeutet streng genommen nicht viel. Die Angabe bedeutet lediglich, dass man sich darauf verlassen kann, dass garantiert kein Preis um mehr als 70% reduziert worden ist. Manche Preise sind vielleicht um 5% reduziert worden, manche vielleicht auch um 10%, aber mit Sicherheit ist kein Preis z.B. um 80% reduziert worden.
Der Wert 70% ist hier die Obergrenze oder obere Schranke für den Preisnachlass: "bis zu" bedeutet " ".
".
| |
| Bild 1: Preise bis zu 70% reduziert | |
Das Missverständnis, dem wir gern erliegen, ist durchaus beabsichtigt: Wir gehen davon aus, dass die obere Schranke auch angenommen wird, d.h. dass es tatsächlich Preise gibt, die um 70% reduziert worden sind.
Sehr beliebt und werblich sicher erfolgreich ist die Ankündigung
Preisnachlass bis zu 70% und mehr
Hier ist die Aussage, dass der Preisnachlass garantiert  70% ist, in einigen Fällen sogar
70% ist, in einigen Fällen sogar  80%. Beides trifft z.B. für einen Preisnachlass von 10% zu. Sowohl 70% als auch 80% sind obere Schranken für den Preisnachlass.
80%. Beides trifft z.B. für einen Preisnachlass von 10% zu. Sowohl 70% als auch 80% sind obere Schranken für den Preisnachlass.
Bei einem Algorithmus bedeutet die Angabe
Zeitkomplexität O(n2)
nicht, dass der Algorithmus quadratische Zeitkomplexität hat. Die Angabe bedeutet nur, dass der Algorithmus höchstens quadratische Zeitkomplexität hat. Er könnte tatsächlich z.B. lineare Zeitkomplexität haben, also eine Zeitkomplexität von O(n). Damit hat er automatisch eine Zeitkomplexität von O(n2), denn es gilt O(n) 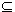 O(n2)
O(n2)
Die Angabe O(n2) ist eine obere Schranke für die Zeitkomplexität des Algorithmus. Dies wird durch das Symbol O ausgedrückt. Häufig genügt uns die Angabe einer oberen Schranke; wir sind zufrieden, wenn der Algorithmus höchstens quadratische Zeitkomplexität hat – ist er schneller, umso besser.
Untere Schranken
Ebenfalls in der Werbung findet man Preisangaben wie
T-Shirts ab 9,95
Diese Angabe bedeutet, dass von den angebotenen T-Shirts garantiert keines weniger als 9,95 kostet. Die meisten kosten 14,95, manche sogar 19,95. Die Angabe 9,95 ist lediglich eine untere Schranke für den Preis: "ab" bedeutet " ". Als Kunden gehen wir natürlich davon aus, dass die untere Schranke auch angenommen wird, d.h. dass es tatsächlich T-Shirts zu 9,95 gibt.
". Als Kunden gehen wir natürlich davon aus, dass die untere Schranke auch angenommen wird, d.h. dass es tatsächlich T-Shirts zu 9,95 gibt.
Die Tatsache, dass ein Algorithmus z.B. mindestens quadratische Zeitkomplexität hat, wird durch das Zeichen Ω ausgedrückt
Zeitkomplexität Ω(n2)
Der Algorithmus kann tatsächlich quadratische Zeitkomplexität haben, möglicherweise aber auch kubische Zeitkomplexität oder sogar exponentielle Zeitkomplexität.
Θ
Wie aber drückt man es aus, dass ein Algorithmus tatsächlich quadratische Zeitkomplexität hat? Hierzu dient das Zeichen Θ (Theta). Es gilt
Θ(n2) = Ω(n2)  O(n2)
O(n2)
Ein Algorithmus, der sowohl mindestens quadratische Zeitkomplexität hat als auch höchstens quadratische Zeitkomplexität, hat tatsächlich genau quadratische Zeitkomplexität. Er hat dann eine Zeitkomplexität von Θ(n2).
Verwechslungsgefahr
Obere und untere Schranken sind leicht zu verwechseln, deshalb ist hier besondere Genauigkeit geboten. Eine Aussage wie
der Algorithmus hat eine Zeitkomplexität von mindestens O(n)
ist unsinnig, denn sie bedeutet, dass der Algorithmus mindestens höchstens c·n Schritte benötigt.
Entweder soll gesagt werden, dass der Algorithmus mindestens c·n Schritte benötigt, dann ist Ω(n) die richtige Angabe, oder höchstens c·n Schritte, dann ist O(n) die richtige Angabe, oder mindestens c1·n Schritte und höchstens c2·n Schritte, dann ist Θ(n) die richtige Angabe.
Zum Schluss folgt noch ein Beispiel dafür, wie schwierig der Umgang mit "mindestens", "höchstens", "ab", "bis zu" und "bis zu ... und mehr" ist.
| |
| Bild 2: Haltbarkeit eines Dichtungsstreifens | |
Der Hersteller garantiert uns hier, dass der Dichtungsstreifen spätestens nach 8 Jahren undicht wird, vielleicht auch schon früher. Reklamationen sind zwecklos: Wird der Dichtungsstreifen nach einem halben Jahr undicht, kann der Hersteller sagen: "Stand ja drauf, Haltbarkeit weniger als 8 Jahre!". Dafür kann man aber vom Hersteller Ersatz verlangen, wenn der Dichtungsstreifen nach 9 Jahren immer noch dicht ist ... 1)
Aufgaben
Aufgabe 1: Sie haben ein Haarwaschmittel gekauft, das bis zu 90% mehr Glanz verspricht. Nach der Haarwäsche ist Ihr Haar genauso stumpf wie vorher. Können Sie sich beim Hersteller beschweren?
| |
| Bild 3: Bis zu 90% mehr Glanz | |
1) Mittlerweile ist das Zeichen  auf der Packung entfernt worden. Die Haltbarkeit beträgt jetzt genau 8 Jahre.
auf der Packung entfernt worden. Die Haltbarkeit beträgt jetzt genau 8 Jahre.
Weiter mit: [Asymptotische Komplexität] oder
 |
|
|


