Textsuche
Algorithmus von Karp-Rabin
Idee
Das Verfahren von Karp und Rabin [KR 87] ähnelt in gewisser Weise dem naiven Algorithmus, denn das Muster wird mit jedem Textfenster verglichen. Aber statt das Muster an jeder Position symbolweise mit dem Textfenster zu vergleichen, wird nur ein einziger Vergleich durchgeführt, und zwar wird die Signatur des Musters mit der Signatur des Textfensters verglichen. Eine Signatur ist ein möglichst eindeutiges Merkmal.
Beispiel: Das Alphabet ist A = {0, ..., 9}, das Muster p = 1 3 0 8 und die Signaturfunktion ist die Quersumme. Die Quersumme von 1 3 0 8 ist 1 + 3 + 0 + 8 = 12.
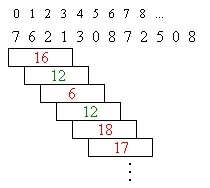
Bild 1: Quersummen in verschiedenen Textfenstern
Die Quersumme des an Position 0 beginnenden Textfensters 7 6 2 1 ist 16. Hier kann also das Muster nicht übereinstimmen. Bei den Textfenstern an den Positionen 1 und 3 stimmt die Quersumme überein. Hier muss geprüft werden, ob das Muster tatsächlich übereinstimmt.
Damit das Verfahren effizient ist, sind an die Signaturfunktion zwei Anforderungen zu stellen:
- Kollisionen sollten möglichst ausgeschlossen sein
- die Signatur muss sich in konstanter Zeit berechnen lassen
Eine Kollision entsteht, wenn die Signatur übereinstimmt, das Muster aber nicht. Wie an obigem Beispiel ersichtlich, ist die Quersumme nicht besonders gut als Signatur geeignet, da sie gegenüber Kollisionen sehr anfällig ist.
Hingegen lässt sich jede Signatur aus der vorhergehenden in konstanter Zeit berechnen: die Zahl, die das Textfenster verlässt, wird subtrahiert, die neu zum Fenster hinzukommende Zahl wird addiert. Wenn das Fenster von Position 0 nach 1 verschoben wird, verlässt 7 das Fenster, 3 kommt hinzu. Die neue Quersumme ergibt sich also aus der alten wie folgt:
16 - 7 + 3 = 12
Signatur
Definition: Sei A ein Alphabet und M eine Menge. Eine Signaturfunktion ist eine Abbildung s : A* → M, die jedem Wort x ∈ A* einen Wert aus s(x) ∈ M zuordnet. Der Wert s(x) ist die Signatur von x.
Definition: Sei s : A* → M eine Signaturfunktion. Eine Kollision ist ein Paar von Wörtern
(x, x') mit x ≠ x' aber s(x) = s(x')
Wie in obigem Beispiel sei A = {0, ..., 9}. Eine bessere Signaturfunktion als die Quersumme ist die durch die Ziffern der Zeichenreihe gebildete Dezimalzahl, also z.B. die Zahl 1308 für die Zeichenreihe 1 3 0 8. Bei dieser Signaturfunktion sind sogar Kollisionen ausgeschlossen.
Die auf diese Weise zustande kommenden Zahlen sollten allerdings jeweils in ein Maschinenwort passen, sodass sie in konstanter Zeit berechnet werden können. Hat die Zeichenreihe eine Länge von höchstens 9 Zeichen, so passt die zugehörige Zahl in ein 32-Bit-Wort. Bei mehr als 9 Zeichen werden nur die letzten 9 Zeichen berücksichtigt, allerdings kann es dann zu Kollisionen kommen.
Diese Signaturfunktion ist formal wie folgt definiert:
s(x0 ... xm-1) =  j = 0, ..., m-1 10 j · xm-j-1 mod 109
j = 0, ..., m-1 10 j · xm-j-1 mod 109
Die Signatur s' des Textfensters ti+1 ... ti+m wird aus der Signatur s des vorhergehenden Fensters ti ... ti+m-1 wie folgt berechnet:
s' = ((s – 10m-1·ti)·10 + ti+m) mod 109
Diese Signaturfunktion ist auch für größere Alphabete mit mehr als zehn Zeichen anwendbar, allerdings mit größerer Gefahr von Kollisionen.
Die folgende Implementation des Karp-Rabin-Algorithmus führt entsprechende Berechnungen zur Basis 2 modulo 232 durch.
Algorithmus
Die Multiplikation mit 2 wird durch eine Linksschiebe-Operation realisiert. Die Multiplikation mit 2m-1 kann nicht durch Linksschieben um m-1 realisiert werden, jedenfalls nicht, wenn m≥32 ist. In der 32-Bit-Arithmetik von Java werden Schiebedistanzen modulo 32 gerechnet. Statt z.B. um 34 würde also um 2 geschoben werden. Es wird daher eine Variable h = 2m-1 mod 232 benötigt. Die Operation mod 232 wird implizit durch die 32-Bit-Zahlendarstellung bewirkt.
Wiederum wird angenommen, dass der Preprocessing- und der Suchalgorithmus in einer Klasse KarpRabin gekapselt sind. In der Klasse sind die Integer-Variablen h und sp deklariert. Die Variable sp enthält die Signatur des Musters.
Karp-Rabin-Preprocessing
{
int i;
h=1; sp=p[0];
for (i=1; i<m; i++)
{
h<<=1;
sp=(sp<<1)+p[i];
}
}
Karp-Rabin-Suchalgorithmus
{
int i, st=0;
for (i=0; i<m; i++)
st=(st<<1)+t[i];
for(i=m; i<n; i++)
{
if (sp==st && matchesAt(i-m)) report(i-m);
st=(st-t[i-m]*h<<1)+t[i];
}
if (sp==st && matchesAt(n-m)) report(n-m);
}
Die Funktion matchesAt vergleicht das Muster mit dem an Position i beginnenden Textfenster auf eine beliebige Weise. Im Suchalgorithmus wird matchesAt jedoch nur dann aufgerufen, wenn die Signaturen des Musters und des Textfensters übereinstimmen.
Analyse
Der Preprocessing-Algorithmus benötigt Θ(m) Schritte. Der Suchalgorithmus benötigt im schlechtesten Fall Θ(n·m) Schritte, z.B. wenn p = am und t = an. Im Durchschnitt allerdings hat der Algorithmus eine Komplexität von Θ(n).
Literatur
[KR 87] R. Karp, M. Rabin: Efficient Randomized Pattern-Matching Algorithms. IBM Journal of Research and Development 31, 249-260 (1987)
Weiter mit: [Shift-And-Algorithmus] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 20.03.2001 Updated: 05.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden