Graph
Vertex and edge
Definition: A directed graph is a pair G = (V, E) where V is a finite set of vertices and E ⊆ V × V a relation on V, the set of edges.
Representation of graphs: The vertices are drawn as points, the edges as arrows, where an arrow is drawn from vertex u ∈ V to vertex v ∈ V if (u, v) ∈ E.
Example: G1 = (V, E) with V = {0, 1, 2, 3, 4} and E = {(0,1), (0,2), (3,0), (2,0), (1,2)}
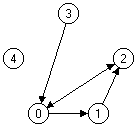
Figure 1: Representation of graph G1
Definition: Let G = (V, E) be a graph and u ∈ V be a vertex. A vertex v ∈ V is called adjacent to u, if there exists an edge from u to v, i.e. if (u, v) ∈ E.
The out-degree o(u) of a vertex u is the number of vertices v adjacent to u, i.e.
o(u) = | { v | (u, v) ∈ E } |
The in-degree i(u) of a vertex u is the number of vertices v it is adjacent to, i.e.
i(u) = | { v | (v, u) ∈ E } |
A vertex u is isolated if o(u) = i(u) = 0.
Example: In G1 vertex 0 is adjacent to vertex 3; vertex 2 has out-degree 1 and in-degree 2. Vertex 4 is isolated.
Path
Definition: A walk in a graph is a finite sequence of edges
p = (u0, v0) ... (um-1, vm-1)
with m ∈ ℕ0 and vi-1 = ui for all i ∈ {1, ..., m-1}.
m is the length of the walk. The walk of length 0 is called the empty walk. Vertex u0 is called start vertex of p, vertex vm-1 is called end vertex of p. All other vertices of p are called inner vertices of p.
Example:
p1 = (3,0) (0,2) (2,0) (0,2)
p2 = (0,1) (1,2) (2,0)
p3 = (3,0)
p4 = (3,0) (0,1) (1,2) (2,0)
are walks in the above graph G1.
Walk p1 has a length of 4, walk p3 has length 1. In walk p2 vertex 0 is start and end vertex. In p4 vertex 0 is inner vertex and end vertex.
Definition: Let p = (u0, v0) ... (um-1, vm-1) be a walk in a graph G.
- p is a trail if it contains each edge at most once, i.e. if all (ui, vi) are different (i = 0, ..., m-1);
- p is called a circuit if it is closed, i.e. if vm-1 = u0;
- p is a path, if it contains each vertex at most once, i.e. if all ui among each other and all vj among each other are different (i, j = 0, ..., m-1);
- p is a cycle, if it is a closed path, i.e. if it is a circuit with no repetitions of vertices.
Example: In G1 walk p1 is not a trail since it contains edge (0,2) more than once. Walk p4 is a trail but no path since it visits vertex 0 more than once. Walk p2 is a circuit and even a cycle.
Tree
Definition: A directed graph T = (V, E) is a tree if
- it contains no cycles,
- there is exactly one vertex r with in-degree 0, the root of the tree, and
- all other vertices have in-degree 1.
Definition: Let T be a tree with root r. A vertex v is called a direct descendant of a vertex u, if it is adjacent to u, i.e. if there is an edge from u to v. A vertex w is a descendant of u, if there is a non-empty path from u to w.
A vertex b is a leaf if it has no descendants; all other vertices are inner vertices of T.
The depth d(v) of a vertex v is the length of the path from the root r to v. The depth d(T) of the tree is the maximum depth of all vertices.
Definition: A tree T is a binary tree if each vertex has an out-degree of at most 2.
A binary tree is called almost complete if
- all vertices of depth < d(T)-1 have out-degree 2, and
- at most one vertex has out-degree 1.
An almost complete binary tree T with n vertices has depth d(T) = int(log(n)).
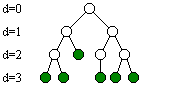
Figure 2: Almost complete binary tree with 12 vertices
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 17.03.2000 Updated: 10.02.2023