Arithmetik
Karatsuba-Multiplikation
Die Schulmethode der Multiplikation von zwei m-Bit-Zahlen a und b ist zwar die einfachste, aber nicht die effizienteste Methode. Die Zeitkomplexität der Schulmethode beträgt Θ(m2). Dies liegt daran, dass eine parallelogrammförmige Tabelle mit m Zeilen der Länge m erzeugt wird. Jedes Bit des Operanden a wird mit jedem Bit des Operanden b multipliziert und anschließend werden die m2 Zwischenergebnisse addiert.
Bild 1: Schulmethode der Multiplikation 9·11 = 99
Divide-and-Conquer-Ansatz
Es liegt nahe, zu versuchen, die Berechnung mittels der Divide-and-Conquer-Strategie zu beschleunigen. Die beiden m-Bit-Zahlen a und b werden jeweils in der Mitte aufgeteilt, also dargestellt als a = a1·2k + a0 und b = b1·2k + b0. Hierbei ist k = m div 2. Das Teilstück a1 enthält die m-k höherwertigen Bits und das Teilstück a0 die k niederwertigen Bits von a (Bild 2). Entsprechendes gilt für b.
zu beschleunigen. Die beiden m-Bit-Zahlen a und b werden jeweils in der Mitte aufgeteilt, also dargestellt als a = a1·2k + a0 und b = b1·2k + b0. Hierbei ist k = m div 2. Das Teilstück a1 enthält die m-k höherwertigen Bits und das Teilstück a0 die k niederwertigen Bits von a (Bild 2). Entsprechendes gilt für b.

Bild 2: Aufteilung der Zahlen a und b in Teilstücke a1 und a0 sowie b1 und b0
Das Produkt c = a · b ergibt sich dann als
c = a1·b1 ·22k + (a0·b1 + a1·b0)·2k + a0·b0
Die einzelnen Teilprodukte lassen sich schneller berechnen, da die Operanden nur die halbe Länge haben, nämlich in Zeit Θ((m/2)2) = Θ(m2/4), also in einem Viertel der Zeit der ursprünglichen Berechnung. Da aber vier dieser Teilprodukte zu berechnen sind, ist leider nichts gewonnen.
Der Trick des Karatsuba-Algorithmus (nach A. Karatsuba ) besteht darin, die obige Formel so umzuformen, dass sie nur noch aus drei Teilprodukten besteht.
) besteht darin, die obige Formel so umzuformen, dass sie nur noch aus drei Teilprodukten besteht.
Idee
Die Formel für die Berechnung des Produkts c wird folgendermaßen umgeformt:
c = a1·b1 ·22k + (a0·b1 + a1·b0)·2k + a0·b0
= a1·b1 ·22k + ((a1 + a0) · (b1 + b0) – a1·b1 – a0·b0)·2k + a0·b0
In der zweiten Zeile sind nur noch drei Multiplikationen erforderlich:
| a1·b1 |
| (a1 + a0) · (b1 + b0) |
| a0·b0 |
Die Teilprodukte a1·b1 und a0·b0 werden nur einmal ausgerechnet und dann in der Formel mehrfach verwendet. Dafür sind eine Addition und zwei Subtraktionen hinzugekommen, aber diese erfordern nur höchstens linearen Aufwand und sind damit auch zusammengenommen deutlich schneller als eine Multiplikation.
Umsetzung
Die Aussage, dass eine Addition und zwei Subtraktionen schneller als eine Multiplikation sind, stimmt natürlich erst ab einer Operandenlänge von k > 3.
Es bietet sich an, den Karatsuba-Algorithmus rekursiv zu implementieren, d.h. die drei Teilprodukte ebenfalls mit dem Karatsuba-Algorithmus zu multiplizieren. Aber spätestens ab einer Länge von ≤ 3 werden die Operanden dann nicht mehr weiter rekursiv behandelt, sondern direkt nach der Schulmethode miteinander multipliziert.
In der Praxis wird bei der Multiplikation von Langzahlen die Rekursion dann beendet, wenn die Operanden mit dem normalen Multiplikationsbefehl des Computers multipliziert werden können.
Programm
Das folgende Python-Programm veranschaulicht die Multiplikation von zwei großen ganzen Zahlen mit dem Karatsuba-Algorithmus. Die höherwertigen Teilstücke von a und b werden durch Rechtsschieben um k Bit erzeugt; die niederwertigen Teilstücke werden durch Maskieren mit k Einsen erzeugt. Die mehrfach verwendeten Produkte a1·b1 und a0·b0 werden in Variablen p2 und p0 gespeichert. Die Rekursion wird hier bei einer Operandenlänge von 16 Bit beendet.
Die anfängliche Abfrage, ob einer der Operanden gleich 0 ist, vermeidet unnötige rekursive Aufrufe in Fällen, wenn die Längen der Operanden a und b sich stark unterscheiden; dann nämlich ist a1 bzw. b1 in den rekursiven Aufrufen häufig gleich 0. Für die Korrektheit erforderlich ist die Abfrage nicht.
if a==0 or b==0:
return 0
m=max(a.bit_length(), b.bit_length())
if m<=16:
return a*b
else:
k=m//2
a1=a>>k
a0=a & (1<<k)-1
b1=b>>k
b0=b & (1<<k)-1
p0=karatsuba_mul(a0, b0)
p1=karatsuba_mul(a1+a0, b1+b0)
p2=karatsuba_mul(a1, b1)
c0=p0
c1=p1-p2-p0 << k
c2=p2 << 2*k
return c0+c1+c2
# Test
if __name__=="__main__":
a=123456789012345678901234567890
b=987654321098765432109876543210
print a, b
print a*b
print karatsuba_mul(a, b)
Zeitkomplexität
Das Programm enthält eine Anzahl von Operationen der Komplexität O(k), wie etwa Schiebeoperationen, Additionen und Subtraktionen von k-Bit-Operanden. Darüber hinaus enthält es drei rekursive Aufrufe mit Operanden der Länge k.
Mit k = m/2 gilt damit
T(m) = 3·T(m/2) + c·m/2
Die Auflösung dieser Rekurrenz ergibt
T(m) ∈ O(3log m)
Verblüffenderweise gilt
3log m = mlog 3
Denn mit den Logarithmen-Formeln x = 2log x und (2x)y = 2x·y gilt
3log m = (2log 3)log m = 2log 3 · log m = 2log m · log 3 = (2log m)log 3 = mlog 3
Da log(3) 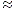 1,585, ist die Karatsuba-Multiplikation mit der Komplexität O(m1,585) wesentlich schneller als die Schulmethode mit der Komplexität Θ(m2).
1,585, ist die Karatsuba-Multiplikation mit der Komplexität O(m1,585) wesentlich schneller als die Schulmethode mit der Komplexität Θ(m2).
Literatur
[Knu 01] D.E. Knuth: Arithmetik. Springer (2001)
[DMS 14] M. Dietzfelbinger, K. Mehlhorn, P. Sanders: Algorithmen und Datenstrukturen. Springer Vieweg (2014)
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 11.09.2018 Updated: 22.06.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden